Рассмотрим участок окружности из второго октанта jc€ [0,RHllye [RHlyR].
Особенностью данного участка является то обстоятельство, что угловой коэффициент касательной к окружности не превосходит 1 по модулю, а точнее, лежит между -1 и 0.
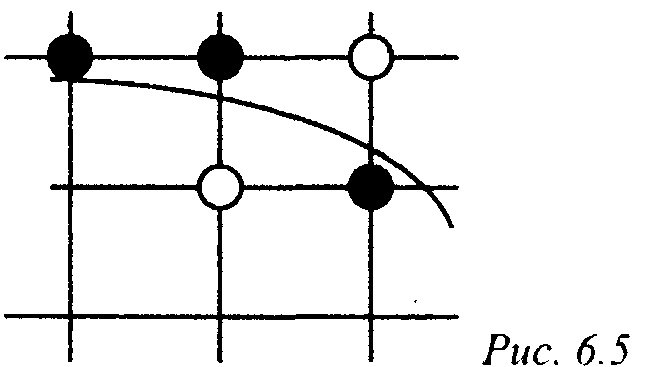
Применим к этому участку алгоритм средней точки (midpoint algorithm).
9 9 9Функция F(jc, у)-х + у - R , определяющая окружность, обращается в нуль на самой окружности, отрицательна внутри окружности и положительна вне ее.
Пусть точка (jcj, у) уже поставлена. Для определения того, какое из двух значений у (у{ или) следует взять в качестве yi+i, введем переменную
dx = F(Xi +\,У1- Vi) = (*j + l)2 + (Vi - Уг)2 -R\
В случае, когда dj < 0, полагаем yj+i = у^Тогда
= F{xx + 2, yx - Уг) - + 2)2 + (vi ~ У2)2 ~ R\ Ac/j = dl+i - d\ ~ 2x\ + 3.
В случае, когда dt ^ 0, делаем шаг вниз, выбирая ^+1=^+1. Тогда di+i = F(jCj + 2,у-{ - 3/2) = (jcj + 2)2 + (y{ - 3/2)2 - R2, Ac/i = 2(jCi-^) + 5
Таким образом, мы определили итерационный механизм перехода от одного пиксела к другому. В качестве стартового пиксела берется. Тогда d0 = F(\,R-V2) = 5/4-R
и мы приходим к алгоритму
О1
lmJ // File Cirdel .Cpp
static int xCenter;
static int yCenter;
static void circlePoints (int x, int y, int color) {6. Растровые алгоритмь
putpixel ( xCenter + х, yCenter + у, color); putpixel ( xCenter + y, yCenter + x, color); putpixel ( xCenter + y, yCenter - x, color); putpixel ( xCenter + x, yCenter - y, color); putpixel ( xCenter - x, yCenter - y, color); putpixel ( xCenter - y, yCenter - x, color); putpixel ( xCenter - y, yCenter + x, color); putpixel ( xCenter - x, yCenter + y, color);
}
void circle 1 (int xc, int yc, int r, int color)
" {
int x = 0; int y = r;
float d = 1.25 - r;
xCenter = xc; yCenter = yc;
CirclePoints (x, y, color);while (у > x)
- (
if ( d < 0 ) {
d += 2*x + 3; x++;
}
else
{d += 2*(x - у ) + 5; x++;
y~;
}
CirclePoints ( x, y, color);
}
}Заметим, что величина dj всегда имеет вид 1А + z,z&Z, и, значит, изменяется только на целое число. Поэтому дробную часть (всегда рав ную 1/4) можно отбросить, перейдя тем самым к полностью целочисленному алго ритму.
