4. Реализуйте окна с прозрачными (полупрозрачными) фрагментами. Реализуйте окна с полупрозрачными тенями.

Глава 6
РАСТРОВЫЕ АЛГОРИТМЫ
Подавляющее число графических устройств являются растровыми, представляя изображение в виде прямоугольной матрицы (сетки, целочисленной решетки) пикселов (растра), и большинство графических библиотек содержат внутри себя достаточное количество простейших растровых алгоритмов, таких, как:
переведение идеального объекта (отрезка, окружности и др.) в их растровые образы;
обработка растровых изображений.
Тем не менее часто возникает необходимость и явного построения растровых алгоритмов.
Достаточно важным понятием для растровой сетки является связность - возможность соединения двух пикселов растровой линией, т. е. последовательным набором пикселов. Возникает вопрос, когда пикселы (х\,у\) и (х^уг) можно считать соседними.
Вводится два понятия связности:
4-связность: пикселы считаются соседними, если либо их ^-координаты, либо их ^-координаты отличаются на единицу:
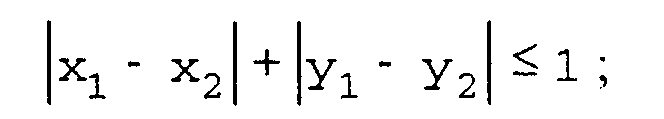
8-связность: пикселы считаются соседними, если их ^-координаты и у координаты отличаются не более чем на единицу:
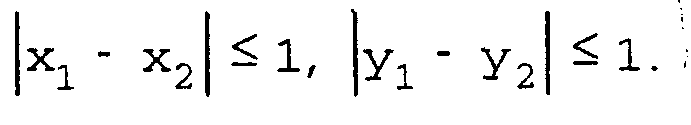
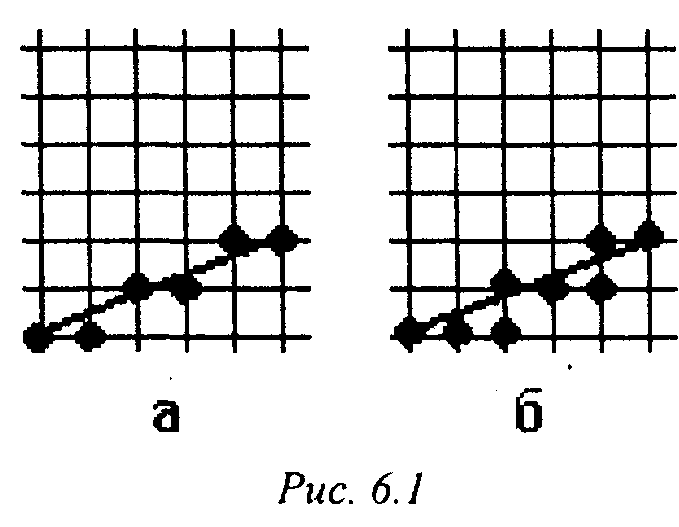
Понятие 4-связности является более сильным: любые два 4-связных пиксела являются и 8-связными, но не наоборот. На рис. 6.1 изображены 8-связная линия (а) и 4-связная линия (б).
В качестве линии на растровой сетке выступает набор пикселов Рь Р2,…, Рп, где любые два пиксела являются сосед ними в смысле заданной связности.
Замечание. Так как понятие линии базируется на понятии связности, то естественным образом возникает понятие 4- и 8-связных линий. Поэтому, когда мы говорим о растровом представлении (например, отрезка), следует ясно понимать, о каком именно представлении идет речь. В общем случае растровое представление объекта не является единственным и возможны различные способы его построения.
6. Растровые алгоритмы
6.1. Растровое представление отрезка. Алгоритм Брезенхейма Рассмотрим задачу построения растрового изображения отрезка, соединяющего точки А(ха, у а) и В(хь, у і). Для простоты будем считать, что 0 < уъ - уа < ->ка . Тогда отрезок описывается уравнением
