Этот шейдер включен в книгу как еще один пример возможностей языка шейде-ров OpenGL: вычисления, ранее возможные только на основном процессоре, сегодня можно выполнять на графическом акселераторе, что дает большой выигрыш в производительности, так как могут обрабатываться несколько пикселов одновременно. Визуализация сложной математической функции, подобной множеству Мандельброта, - только верхушка айсберга в использовании программируемых шейдеров для визуализации математических формул и научных объектов.

15.3.1. О множестве Мандельброта Чтобы понять, что такое множество Мандельброта, нужно вспомнить несколько понятий высшей математики. Существует число, называемое мнимым и обозначаемое г, определенное как результат квадратного корня из -1.

С использованием мнимого числа может быть описан результат квадратного корня любого отрицательного числа. Например, (Зг)2 = -9, и наоборот, 7^9 = Зг Числа, состоящие из вещественной и мнимой частей, например 6 + 4г, называются комплексными числами. Над комплексными числами можно выполнять обычные арифметические операции. Результат умножения двух комплексных чисел следующий: х = а + Ы; у - с + di\ ху = ас + adi + cbi -bd= (ас - bd ) -1 (ad + bc)i.

15.3. Пример Мандельброта Так как комплексные числа состоят из двух частей, множество комплексных чисел является двухмерным. Их можно обозначить на плоскости, где горизонтальная ось представляет вещественную часть числа, а вертикальная - мнимую (рис. 15.6).

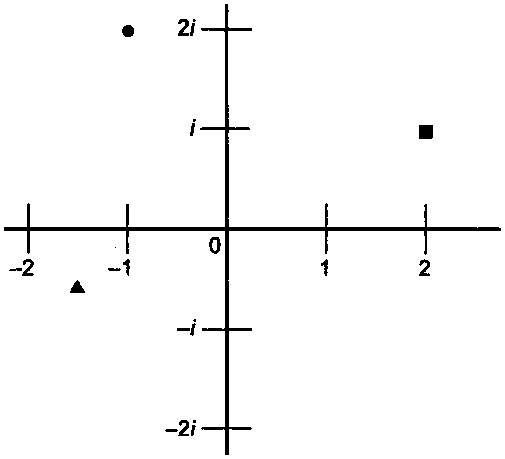
Рис. 15.6. Пример обозначения комплексных чисел на плоскости На рис. 15.6 показаны три точки на плоскости"opengl2_340.html">⇐ Предыдущая| |Следующая ⇒