14.4.3. Адаптивный аналитический предварительный отбор
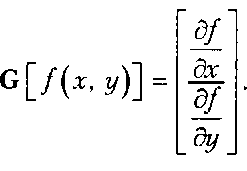
Сглаживание процедурных текстур
Значение модуля градиентного вектора функции /(х, у) обычно называется градиентом функции /(х, у). Он определен как таё[с[/(х, у)]] = щл((д//дх)2 +(д//ду)2)На самом деле не всегда нужно выполнять громоздкие вычисления квадратного корня. Градиент можно подсчитать приблизительно, вычислив абсолютные значения: тав[с[/(х, г/)]] =аЦ/(.г, у)- /(х +1, у)) + а!*,(/(.г, у)- /(х, г/ +1))В результате получится значение, которое возвращает обычная встроенная функция Ты1сИИ. Сумма абсолютных значений является верхней границей фильтра. Если это значение слишком велико, окончательное изображение будет размытым больше, чем нужно, но обычно степень размытия вполне приемлема.
Два метода вычисления градиента сравниваются на рис. 14.5. Как можно заметить, существует небольшое видимое различие результата. Так как значение градиента слишком маленькое для функции этого объекта, значения были масштабированы.
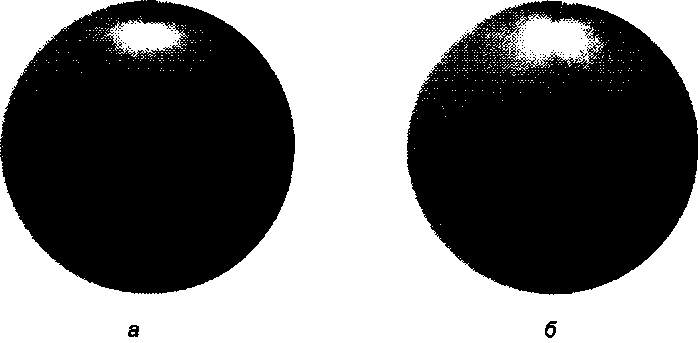
Рис. 14.5. Визуализация градиента: а - модуль вектора градиента используется как значение интенсивности цвета; б- градиент вычислен приближенно (реальные значения градиента масштабированы)1
Чтобы вычислить фактический градиент для varying-переменной V во фрагментом шейдере, используем следующий код: float width = length(vec2 (dFdx(V). dFdy(V))): Вычислим более приблизительное значение, но быстрее: float width = fwidth(V): Ширина фильтра затем передается в функцию smoothstep таким образом: float edge = width * 32.0:
float square = smoothstep(0.5 - edge. 0.5 + edge, triangle):Фрагментный шейдер, выполняющий все это, приведен в листинге 14.1.
1 Рисунок любезно предоставлен Бертом Фрейденбергом, университет Магдебурга, 2002.
14.4. Пример сглаживания полосок Листинг 14.1. Фрагментный шейдер для адаптивного аналитического сглаживания
varying float V: // произвольное число
varying float Lightlntensity:uniform float Frequency: // частота полосок равно 6
void main (void) {
float sawtooth = fractCV * Frequency); float triangle = abs(2.0 * sawtooth - 1.0): float dp = length(vec2 (dFdx(V). dFdy(V))): float edge = dp * Frequency * 2.0: