Преобразование из пространства координат объекта в локальное пространство координат поверхности показано на рис. 11.3. Вектор пространства координат объекта (Ох, Оу, Ог) преобразуется в локальное пространство умножением на матрицу, в которой содержится тангенциальный вектор (Тх, Ту, Г2) в первой строке, вектор бинормали (В.г, Вц, Вг) во второй строке и нормаль поверхности (Н*, ЛГ,, Л1^) в третьей строке. Можно использовать этот способ для преобразования и вектора освещения, и вектора обзора. Преобразованные векторы будут интерполированы в пределах примитива, а интерполированные векторы затем используются во фрагментном шейдере для вычисления отражения с помощью уже измененной нормали.

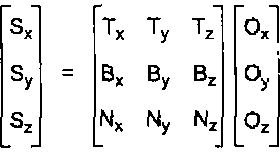
Рис. 11.3. Преобразование из пространства координат объекта в локальное пространство координат поверхности

11.4.1. Подготовка приложения Чтобы шейдер бугристой поверхности работал правильно, приложение должно задать координаты вершины, нормаль поверхности и тангенциальный вектор в плоскости поверхности. Тангенциальный вектор передается как произвольный вершинный атрибут, а индекс атрибута должен быть связан с переменной вершинного шейдера tangent с помощью вызова функции gl В1 ndAttri bLocationARB. Приложение также должно задать значения для uniform-переменных Li ghtPosi ti on, SurfaceColor, BumpDensity, BumpSize и SpecularFactor.

Необходимо позаботиться о том, чтобы тангенциальные векторы были согласованы; в противном случае преобразования в локальные пространства также будут несогласованными, что сделает результаты вычисления освещения непредсказуемыми. Согласованные тангенциальные векторы могут быть вычислены алгоритмически для поверхностей, определенных математическими формулами, Согласованные тангенциальные векторы для сложных объектов можно вычислить с помощью соседних вершин, согласованно упорядочивая их с помощью текстурных координат объекта.

Проблема, связанная с несогласованно определенными нормалями, иллюстрируется рис. 11.4. На диаграмме показаны два треугольника"opengl2_274.html">⇐ Предыдущая| |Следующая ⇒