Функция ftransform предназначена для вычисления gl_Position таким образом:
gl_Position = ftransformOОна преобразует значение glj/ertex, используя текущую матрицу модели-вида, чтобы вычислить для gl _Posi ti on значение, идентичное тому, что было бы вычислено с помощью стандартных операций OpenGL. Эта функция используется, например, когда приложение обрабатывает одни и те же геометрические фигуры за несколько проходов, и один проход выполняется с помощью стандартных операций, а другой - с использованием программируемых процессоров.
5.5. Матричные функции Матричные функции могут вызываться как из вершинных, так и из фрагментных шейдеров (табл. 5.5).
ПримечаниеЧтобы получить результат математического умножения матриц, следует использовать оператор умножения (*).
Встроенные функции
Таблица 5,5. Матричные функции
|
Синтаксис |
Описание |
|
таі2 та1:п"хсопіршИ |
Умножает матрицу л-на матрицу /покомпонентно, |
|
таі2 х, таЬ2 у) |
то есть, твиК [г][Л является скалярным |
|
таіЗ ш№хсояртии |
произведением х[Ц[/\ на /[<][;']. |
|
тЬЗ х. таї-З у) |
|
|
таЬ4 П1atгi хсотртиі t |
|
|
таі4 х. таі4 у) |
Эти функции выполняют покомпонентное умножение двух матриц. Например, результат вызова функции таІтіхсотрглиН с двумя ЗО-матрицами х и у будет выглядеть так:
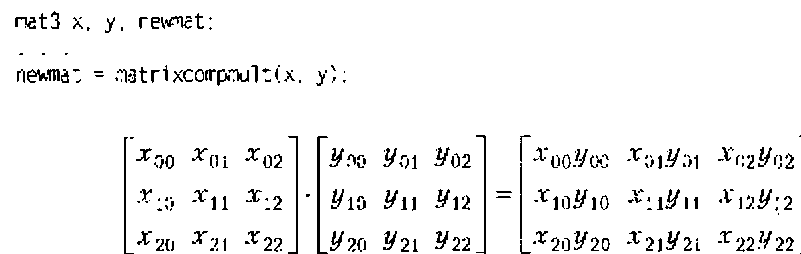
Обычно это не те действия над матрицами, которые необходимы для преобразований. Нужно использовать оператор умножения (*), чтобы выполнить математическое умножение матриц: лпаіЗ х. у. пемпат.: пемгнг = х * у: При этом будет выполняться следующая операция:
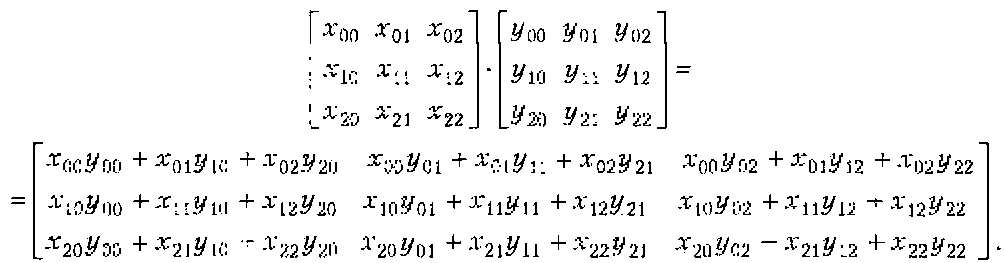
5.6. Функции отношения векторов Операторы равенства и отношения (<, <=, >, >=, ==,. 1=) определены таким образом, чтобы возвращать скалярные логические значения, они могут использоваться как из вершинных, так и из фрагментных шейдеров. Для векторов следует воспользоваться одной из перечисленных далее встроенных функций (табл. 5.6).
5,6. Функции отношения векторов Таблица 5.6. Функции отношения векторов
|
Синтаксис |
Описание |
|
Ьуєсй lessThan(vec2 x. vec2 y) |
Возвращает результаты покомпонентного |
| bvec3 lessThan(vec3 x. vec3 y) |
сравнения х < у |
| bvec4 lessThan(vec4 x. vec4 y) | |
| bvec2 lessThan(ivec2 x. ivec2 y) | |
| bvec3 lessThandvecS x, ivec3 y) | |
| bvec4 lessThan(ivec4 x, ivec4 y) | |
| byec2 lessThanEqual(vec2 x, vec2 y) |
Возвращает результаты покомпонентного |
| bvec3 lessThanEquaKvec3 x, vec3 y) |
сравнения х< у |
| bvec4 lessThanEqual(vec4 x. vec4 y) | |
| bvec2 lessThanEquaKivec2 x. ivec2 y) | |
| bvec3 lessThanEqual(ivec3 x, ivec3 y) | |
| by.ec4 lessThanEquaKivec4 x, ivec4 y) | |
| bvec2 greaterThan(vec2 x. vec2 y) |
Возвращает результаты покомпонентного |
| bvec3 greaterThan(vec3 x. vec3 y) |
сравнения х> у |
| b.vec4 greaterThan(vec4 x. vec4 y) | |
| bvec2 greaterThan(ivec2 x. ivec2 y) | |
| .bvec3 greaterThan(ivec3 x, ivec3 y) | |
| bvec4 greaterThan(ivec4 x. ivec4 y\ | |
| bvec2 greaterThanEqual(vec2 x. |
Возвращает результаты покомпонентного |
| vec2 y) |
сравнения x^l у |
| bvec3 greaterThanEqual(vec3 x. vec3 y) | |
| bvec4 greaterThanEqual(vec4 x. vec4 y) | |
| bvec? greaterThanEqualfіvec2 x. | |
| 1vec2 y) | |
| bvecS greaterThanEquaKivec3 x.ivec3 y) | |
| bvec4 greaterThanEqual(іvec4 x.ivec4 y) | |
| bvec2 equal(vec2 x, vec2 y) |
Возвращает результаты покомпонентного |
| bvec3 equal(vec3 x. vec3 y) |
сравнения х~ у |
| bvec4 equal(vec4 x. vec4 y) | |
| byec2 equal (ivec2 x, ivec2 y) | |
| bvec3 equal(ivec3 x. ivec3 y) | |
| bvec4 equa!(iveC4 x. ivec4 y) | |
| bvec2 equal(bvec2 x. bvec2 y) | |
|
ЬуесЗ equal(ЬуесЗ x. bvec3 y) |
|
| bvec4 equal(bvec4 x. bvec4 y) | |
| bvec2 notEqual(vec2 x. yec2 y) |
Возвращает результаты покомпонентного |
|
ЬуєєЗ notEqual(vec3 x. vec3 y) |
сравнения Jrt = у |
| bvec4 notEqual(vec4 x. vec4 y) | |
| bvec2 notEqual(іvec2 x. ivec2 y) | |
| bvec3 notEqual(іvec3 x. ivec3 y) | |
| bvec4 notEqual(ivec4 x. ivec4 y) | |
| byec2 notEquaUbvec2 x. bvec2 y) | |
| bvec3 notEqual(bvec3 x, bvec3 y) | |
| bvec4 notEqual(bvec4 x. bvec4 y) | |
| bool any(bve.c2 x) |
Возвращает true, если хотя бы один компонент х |
| bool any(bvec3 x) |
Возвращает true, если хотя бы один компонент х |
| bool any(bvec4 x) |
является true |
| bool all(bv'ec2 x) |
Возвращает true, только если все компоненты х- true |
| bool alUbvec3 x) | |
| bool all(bvec4 x) | |
| bvec2 not(bvec2 x) |
Возвращает результаты покомпонентного отрицания х |
| bvec3 not(bvec3 x) | |
| bvec4 not(bvec4 x) |
