и дает грубую оценку вероятности ложной тревоги: это такая ситуация, когда тест относительно экстента указывает на соударение с лучом, в то время как полный тест обнаруживает прохождение луча мимо объекта. Повторите это упражнение для тестирования прямоугольного экстента.

14.9.2. Разработка теста для сферического экстента Адаптируйте алгоритм пересечения луча со сферой (листинг 14.6) для случая сферы радиуса г с центром в точке center.

14.9.3. Тестирование луча со сферическим экстентом О Покажите, что наименьшая сфера, охватывающая базовый цилиндр с единичным радиусом крышО Покажите, что решение уравнения F(S + ct) - 0 обычно приводит к квадратному уравнению At2 + + 2Bt + С = 0, где А - |с|2, В - с S', С -15'|2 - 1,25, a S' определено как S' - (S^ Sy, 5г - 0,5).

14.9.4. Реализация теста для базового прямоугольного экстента Усовершенствуем метод Cube :: hit() путем разработки подпрограммы

bool rayHitsBoxExtent(Ray& ray, CuboidS cub)

которая проверяет пересечение заданного луча с экстентом, описанном в cub. Это приводит к упрощению метода hit() без изменения его логики. Покажите, что значения переменных numer и denom, необходимых

степень пустоты =

(площадь круга)-(площадь цилиндра)

(площадь круга)

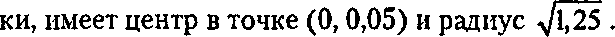
О

Покажите, что уравнение этой сферы в неявной форме имеет вид: ( I \2

Р(х,у,г) = х2 + у2+ 2- -1,25.

2 1

Введение в трассировку лучей

для каждой плоскости бокса, зависят отданных, содержащихся в cub. (Например, для верхней плоскости top используются numer = cub.top-ray.start.у; denom = ray.dir.у.) При пересечении каждой плоскости бокса с лучом возможный интервал (tin, rout) обновляется; если этот интервал становится пустым, то происходит «досрочный выход» и тест возвращает значение false.

14.9.5. Кластер точек для конического цилиндра Покажите, что гексаген, описанный около круга единичного радиуса, должен иметь радиус 4/3. Выведите формулы 12 вершин кластера точек для цилиндра. Напишите метод makeExtentPoi nts (Poi ntCl uster& clust) для класса TaperedCylinder.

⇐ Предыдущая| |Следующая ⇒