Построение сферических и прямоугольных экстентов Для каждого заданного объекта нам необходимо построить сферический и прямоугольный экстенты. Базовые экстенты нужно создавать всего один раз для каждого типа формы, однако мировые экстенты должны делаться заново для каждого экземпляра объекта - с учетом аффинного преобразования, связанного с этим экземпляром. Как, например, найти сферический экстент для циливдра, который был сложным образом масштабирован и повернут?
Один совсем простой метод заключается в том, что с каждой формой ассоциируется кластер точек (point cluster). Это множество точек, выпуклая оболочка которых заключает в себе данный объект. Напомним простой интуитивный способ представить себе выпуклую оболочку некоторой совокупности точек: окружите эти точки воздушным шаром и позвольте этому шару постепенно сдуваться, стягиваясь вокруг них. Получившийся полиэдр и будет выпуклой оболочкой. Имея кластер точек, нетрудно создать сферу, охватывающую этот кластер. Разумеется, такая сфера будет охватывать и исходный объект. (В силу транзитивности, если форма Л охватывает форму В и В охватывает форму С, то А охватывает С.) Мы можем также получить выпуклую оболочку для преобразованного объекта: для этого нужно просто преобразовать каждую точку из кластера, в результате чего получим новые точки, которые и составят преобразованный кластер. Поскольку при аффинных преобразованиях сохраняется «нахождение внутри» («inside-ness»), то если объект А лежит внутри выпуклой оболочки В, то преобразованный объект Т(А) должен лежать внутри выпуклой оболочки Т(В), построенной на преобразованных точках.
Следовательно, нам нужно построить для каждого типа формы кластер точек. Для классов Cube и Square это просто: их собственные вершины и являются этими точками. Просто это и для класса Mesh: в качестве кластера точек здесь используется сам список вершин.
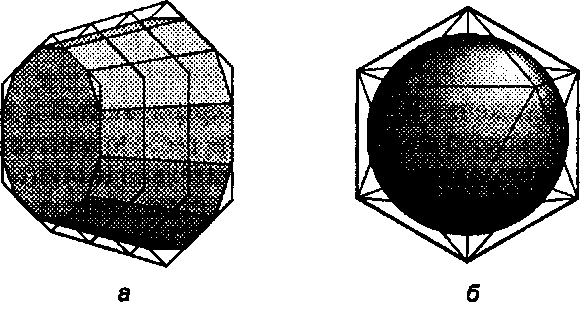
Рис. 14.39. Определение кластеров точек для цилиндра и для сферы
С классами Sphere и TaperedCyl i nder проблем больше, поскольку они определяются скорее через свойства симметрии, чем с помощью точек. Один из приемлемых подходов заключается в том, чтобы заключить каждую форму в плотно охватывающий ее полиэдр и в качестве кластера точек использовать вершины этого полиэдра. На рис. 14.39, а показан базовый конический цилиндр, заключенный в призму, оба основания которой являются гексагонами. Для плотного охвата круглого основания цилиндра радиус гексагена основания должен равняться 4/3 (см. упражнения). Отметим, что такой кластер точек формируется индивидуально для каждого экземпляра конического цилиндра и строится отдельно для каждой специфической формы цилиндра. На рис. 14.39, б приведена базовая сфера, заключенная в икосаэдр, 12 вершин которого составляют кластер точек для этой сферы. Для плотного охвата единичной сферы вершины икосаэдра должны находиться на расстоянии примерно 1,26 от центра сферы (см. упражнения).
