Коэффициенты отражения фонового и диффузного света базируются на коэффициентах Френеля 5(0, Г|г) при нормальном падении. Это всего лишь приближение, которое Кук и Торренс используют для простоты, поскольку отмечено лишь малое изменение значений коэффициента 5(0, г)г) при значениях угла падения ф вблизи нуля, поэтому разумно использовать в качестве приближения значение коэффициента именно при 0 = 0. Отметим, что данный коэффициент имеет различные значения для различных длин волн (то есть «обладает цветом»): зеленая и синяя составляющие зависят соответственно от 5(0, г)я) и от 5(0, г)4) и их значения различны, поскольку показатели преломления различаются для разных цветов.

Введение в трассировку лучей

Член, соответствующий диффузному свету, содержит уже знакомый нам коэффициент Ламберта (см. уравнение (14.22)), а также два других множителя. Член - это пространственный угол, образуемый источником света в точке соударения (рис. 14.22). Для простоты предполагается, что данный член одинаков для всех точек сцены; он обычно выбирается в виде малой константы, например 0,0001. (Солнце образует пространственный угол, равный 0,000068 стерадиан.) Множитель кл (и соответствующий ему коэффициент кз в члене зеркального отражения) характеризует разделение падающего света на диффузную и зеркальную составляющие. Эти два множителя являются свойствами материала и в сумме составляют единицу: ка + к5 = 1. Зеркальный член совпадает с таким же членом из уравнения (14.29), выказывая явную зависимость коэффициента Френеля от длины волны.

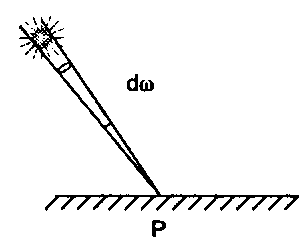
Рис. 14.22. Источник образует пространственный угол аш

Для того чтобы использовать эти формулы, нам необходимо знать коэффициент преломления рассматриваемого материала для различных длин волн. Обычно такая информация недоступна. Однако доступны измеренные значения «нормальной отражательной способности» различных материалов; иными словами, значения коэффициентов ДО, Г)) при различных длинах волн. Кук и Торренс вывели показатель преломления из этих экспериментальных значений посредством следующих рассуждений"opengl1_969.html">⇐ Предыдущая| |Следующая ⇒