Для квадратичных поверхностей, таких как сфера, функция d(t) имеет параболическую форму, а для тора - форму полинома четвертого порядка. Для других поверхностей d(t) может быть настолько сложной, что нам придется определять те значения г, при которых функция d(.) обращается в нуль, численными методами. Рассмотрим, например, суперэллипсоид из табл. 6.11. Этой поверхности соответствует функция
14.6.4. Добавление новых примитивов
dit) = F(S+ct).
(14.18)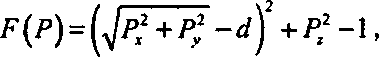
(14.19)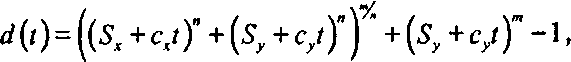
(14.20)Введение в трассировку лучей
где тип - константы, определяющие форму поверхности. Для того чтобы найти наименьшее положительное значение t, обращающее функцию d(t) в нуль, мы вычисляем d(t) для последовательности значений t и определяем среди них такое, при котором d(t) очень мала. При использовании таких алгоритмов, как метод Ньютона [Conte, deBoor, 45], возможно получать все лучшие и лучшие приближения г, но, как правило, численные методы требуют большого числа итераций, что, несомненно, существенно замедляет процесс трассировки луча.
a d№ Луч
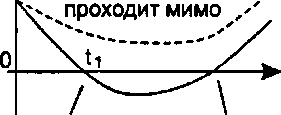
Луч Луч входит в объект выходит из объекта Рис. 14.14. Зависимость функции d(t) от времени t для заданного луча и заданного объекта Были разработаны методы трассировки луча для множества прочих объектов, среди которых важно выделить фрактальные поверхности, поверхности вращения, а также призматические цилиндры [Kajiya, 120]. (См. тематическое задание 14.7, где рассматриваются подходы к трассировке луча для таких объектов.) Поиск эффективных алгоритмов трассировки луча для все большего набора форм является постоянным предметом исследования в графике.
Практические упражнения
14.6.11. Пересечения с тором Посмотрите в математическом справочнике, как находить решение уравнения четвертого порядка, и укажите шаги, которые необходимо выполнить для нахождения одного или нескольких пересечений луча 5 + et с тором, заданным уравнением (14.19).
14.6.12. Трассировка луча для седла (гиперболического параболоида)
Укажите шаги, которые требуются для нахождения пересечений луча 5 + et с гиперболическим параболоидом из табл. 6.10.
