Суть алгоритма Варнока заключается в геометрическом анализе, выполняемом с помощью метода isSimple_drawIt(). Область следует тестировать с каждой гранью из списка граней, чтобы определить, сколько граней втянуто в данную область. Инкапсулируем это тестирование в метод islnvol vedCFace & face), который возвращает true, если грань face втянута в область, и false в противном случае. Чем разумнее составлен данный тест, тем быстрее будет работать рассматриваемый HSR-алгоритм. Какие проверки могут потребоваться в этой функции? Существуют различные ситуации, в которых грань F может быть втянута или не втянута в прямоугольную область R, как показано на рис. 13.14.
О Экстент-непересечение (extent disjoint). Грань F называется экстентно-непересекающейся с областью R, если экстент FHe имеет пересечений с R (рис. 13.14, а). Если грань F3KCTeHTH0 не пересекается с областью R, то F должна целиком лежать вне R. Эта геометрическая ситуация наиболее проста для определения.
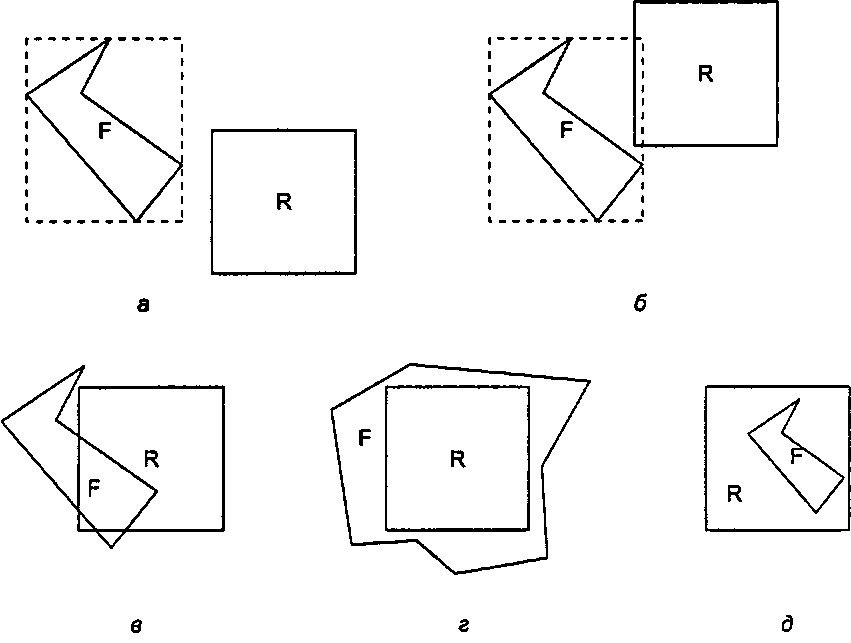
Рис. 13.14. Варианты втянутости грани в область: а) экстент-непересечение; б) непересечение; в) пересечение; г) охватывание; д) заключение внутри
Удаление невидимых поверхностей
О Непересечение (disjoint). Грань Сможет не пересекаться с областью Rt даже когда ее экстент пересекается с этой областью (рис. 13.14, б). Чтобы проверить это условие, нужно произвести отсечение каждого из ребер грани F областью R. Если все ребра грани отсекаются, то они должны лежать целиком вне R и, следовательно, грань F не пересекается с R. Проверка данной ситуации более сложна, чем тест на экстент-непересечение, поэтому данный тест выполняется только тогда, когда тест на экстент-непересечение дал отрицательный результат.
О Пересечение (intersecting). По крайней мере одно ребро грани F пересекает границу области R (рйс. 13.14, в). Позднее мы увидим, как можно объединить тесты на пересечение с тестом на непересечение. Отметим, что пересечение может иметь место даже тогда, когда нй одна из вершин грани F по существу не лежит внутри области R. (Как это может быть?)
