Поэтому поищем более общие семейства стыковочных функций, которые обладали бы всеми свойствами из обсуждавшегося ранее списка пожеланий. Мы будем использовать ту же параметрическую форму:
^(0=Х^Л(0 (11.54)
* =0на базе (L + 1) контрольных точек и (L + 1) стыковочных функций Ra(t),…, RL(t). Остается в силе и требование, чтобы Р(г) была аффинной суммой точек. В качестве стыковочных функций мы будем по-прежнему использовать кусочные полиномы, однако теперь они будут определены в более общей последовательности узлов, именуемой узловым вектором (knot vector):
T-(r0,f,,r2,…). (11.55)Узловой вектор является просто списком узловых значений г0, г2.....для которых предполагается, что они не убывают, то есть г( < г.+1. Некоторые из этих узлов могут иметь одинаковые значения, однако и в этом случае им присваивают отдельные имена. Число узлов, содержащихся в векторе Т, мы рассмотрим позднее.
Рисунок 11.27 иллюстрирует эту ситуацию. Каждая стыковочная функция Rk(f) является кусочным полиномом, который равен нулю до момента времени tk, отличен от нуля на протяжении нескольких диапазонов узлового вектора и затем снова возвращается к нулевому значению. Кроме того, мы требуем, чтобы каждая функция Rt(t) была сплайн-функцией, вследствие чего она будет обладать достаточной степенью гладкости при всех поддерживающих ее значениях г.
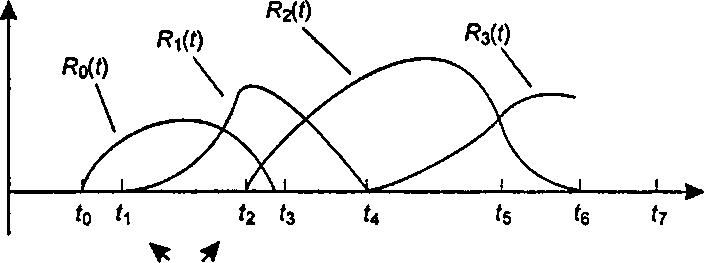
Узловой вектор
Рис. 11.27. Обобщение понятий узлового вектора и стыковочных функций Отметим, что и выражение для кривой Безье, и выражение, содержащее смещения g(t), удовлетворяют следующей общей схеме.
О Кривая Безье. Здесь всего один диапазон - от 0 до 1, все полиномы Бернштейна имеют степень L, имеется L + 1 узел при t - 0 и еще L + 1 узел при г - 1. Полиномы Бернштейна являются сплайнами, поскольку их производные непрерывны до i-ro порядка включительно. __
О Смещения g(t). Узловыми значениями являются целые числа 0, 1.....1 + 2, каждый компонент
g(t - к) является сплайном, состоящим из трех полиномов второй степени, активных в диапазоне шириной 3.
11.7. Базисные функции В-сплайнов
