11.5.2. Нарисуйте скорость
Проставьте на миллиметровке четыре точки, нарисуйте для них кривую Безье и тщательно нарисуйте векторы ее скорости и ускорения как функции от t.
11.5.3. Вывод скорости кривой Безье (сложное упражнение)
Докажите правильность выражения для скорости, приведенного в уравнении (11.37). Подсказка. Покажите, что производная от г*(1 - t)L'k равна ktk-'(1 - t)L~t - (L - k)tk(l- t)L'k'1, поэтому p'(0 можно записать в виде разности двух кривых Безье. Поманипулируйте этими двумя кривыми (например, изменяя индекс суммирования), так чтобы они зависели от одних и тех же полиномов Бернштейна, а затем объедините два члена в один.
11.5.4. Ускорение кривых Безье Поскольку взятие производной от кривой Безье сводится просто к построению кривой Безье на базе первых разностей ее контрольных точек, то вторая производная должна быть кривой Безье, построенной на базе разностей от разностей. Покажите, что ускорение кривой Безье определяется следующей формулой:
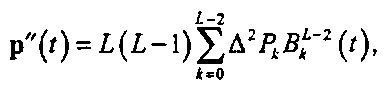
(11.44)где А2Рк~АРк+1-АРк (11.45)
вторые разности контрольных точек. Выразите вторую разность А2Рк через исходные контрольные точки. Найдите общий вид г-й разности контрольных точек и выведите выражение для г-й производной от кривой Безье.
Создание кривых и поверхностей
11.5.5. Сколько раз дифференцируемы кривые Безье L-ro порядка?
Является ли кривая Безье на базе L контрольных точек Z-гладкой кривой? Если да, то докажите это. Если нет, то укажите наивысший порядок непрерывной производной от такой кривой.
11.5.6. Случаи второго и четвертого порядков Найдите матрицу BezL для случаев L - 2 и L - 4.
11.5.7. Выведите элементы матрицы BezL
Покажите, что г/'-й элемент матрицы BezL определяется уравнением (11.43).
11.6. Нахождение лучших стыковочных функций Меня поощряли за быстрые ответы. Я ответил, что не знаю.
Марк Твен (Mark Twain)
Может показаться, что кривые Безье являются наилучшим средством проектирования кривых. При разумном размещении контрольных точек на плоскости можно создать бесконечное разнообразие гладких кривых. Однако далее мы увидим, что сами по себе кривые Безье не обеспечивают достаточной гибкости при конструировании кривых. Одна из проблем состоит в том, что степень используемых полиномов Бернштейна связана с числом контрольных точек: кривая Безье на базе (L + 1) контрольной точки является комбинацией полиномов i-ro порядка. Полиномы высокого порядка сложны в вычислении и чувствительны к ошибкам округления. Мы хотим предоставить дизайнеру свободу выбирать столько контрольных точек, сколько он пожелает, даже 40 и более.
