Нетрудно показать (см. упражнения), что четырехточечная кривая Безье имеет следующую параметрическую форму:

P(t) - Р0(1 - О3 + Р,3(1 -1)4 + Р23(1 - t)t2 + P3t\ (11.21)

что является кубическим полиномом относительно t. Каждой контрольной точке Р. в этом кубическом полиноме придается определенный вес, после чего эти взвешенные точки складываются. Члены, входящие в данный полином, носят название полиномов Бернштейна (Bernstein polynomials). Четыре кубических полинома Бернштейна имеют вид1:

1 Верхний индекс ие означает возведение в куб, а указывает на степень полинома. - Примеч. пер.

Создание кривых и поверхностей

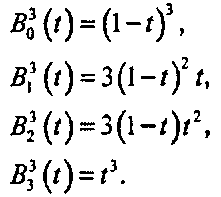
(11.22)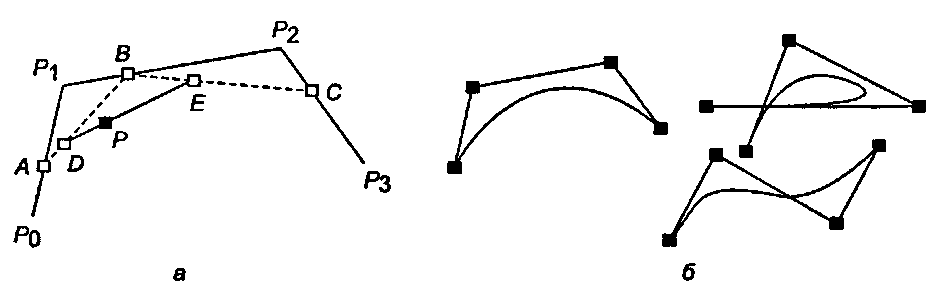

Рис. 11.13. Кривая Безье на базе четырех точек Кубические полиномы Бернштейна легко запомнить, поскольку они совпадают с членами разложения выражения [(1 - 0 + г13> полученными после приведения подобных членов"images/tmp8E4A-751.png">

В таком случае очевидно, что точка P(t) является аффинной комбинацией точек, поэтому эти взвешенные точки можно складывать. (Вспомним задачу сложения точек в главе 4.)

На рис. 11.14 приводятся графики четырех полиномов Бернштейна третьей степени при изменении t от 0 до 1. Видно, что эти полиномы плавно изгибаются по мере изменения t. Позднее мы увидим, насколько они «плавны».

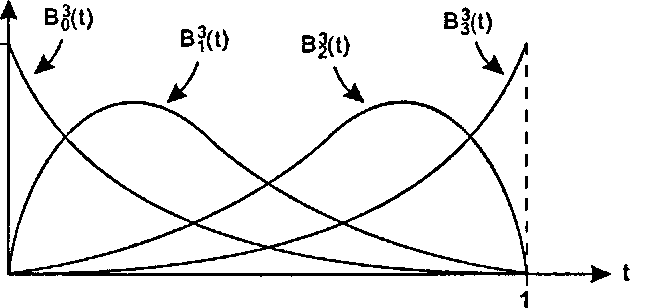
Рис. 11.14. Полиномы Бернштейна третьей степени На рис. 11.15 приведена геометрическая иллюстрация сопряжения четырех точек Р0, Р{, Р2, Р3 из уравнения (11.21) для формирования точки P(t). Если представить эти точки как векторы, исходящие из начала координат (при этом вместо Р0 мы пишем р0 и т. д.), то при t - 0,3 данное уравнение примет вид"opengl1_771.html">⇐ Предыдущая| |Следующая ⇒