где Р0, Р{ и Р2 - три произвольных точки на плоскости. Эти точки в данном контексте носят название контрольных точек (control points), поскольку именно они определяют форму кривой. Уравнение (11.14) в действительности представляет собой два уравнения и является сокращенной записью такого полного выражения:

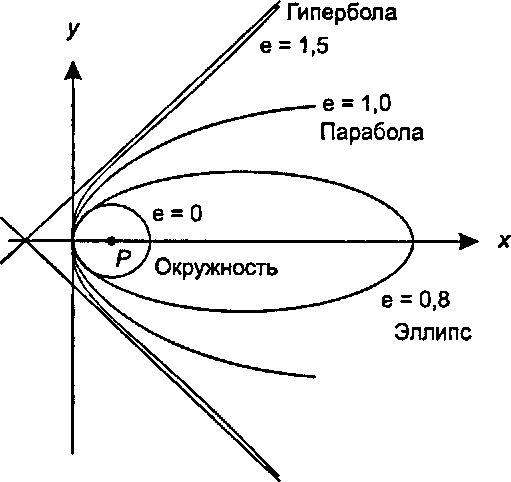
Рис. 11.5. Уравнения конических сечений с общей вершиной

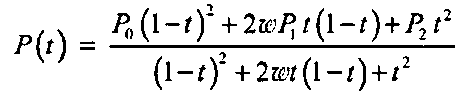
(11.14)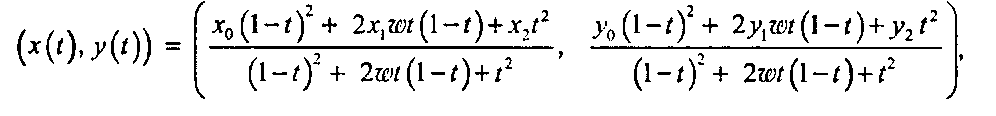

(11.15)

Создание кривых и поверхностей

где х0 и у0 - компоненты точки Р0, и аналогично для двух других точек. Коэффициенты квадратичных полиномов в числителях являются компонентами контрольных точек. Полиномы в знаменателях одинаковы для х(.) и для у(.) и также являются квадратичными, однако не зависят от контрольных точек. В то же время они зависят от «весового» параметра w.

Отметим, что функция P(t) является линейной комбинацией контрольных точек. Как мы уже видели в разделе «Аффинные комбинации точек» главы 4, для того чтобы P(t) приобрела смысл точки, она должна быть аффинной комбинацией этих точек. К счастью, в нашем случае это условие выполняется; подробнее это рассмотрено в упражнениях.

Также отметим, что если подставить в уравнение (11.15) t - О, то его правая часть сократится до выражения (хй, уй)\ следовательно, заданная таким образом кривая проходит через точку Р0, то есть интерполирует (interpolates) ее. Аналогично, при t - 1 кривая проходит через точку Р2. Для всех t, находящихся в промежутке между t - О и t - 1, функция P(t) сложным образом зависит от всех трех точек.

Рисунок 11.6, а, где показаны три контрольных точки, иллюстрирует кривую, исходящую из точки Р0 при нулевом значении t и заканчивающуюся в точке Р2 по достижении параметром t значения 1. Остается открытым вопрос, какую форму эта кривая имеет в промежутке. Ответ дается на рис. 11.6, б"opengl1_764.html">⇐ Предыдущая| |Следующая ⇒