В качестве примера рассмотрим камеру, движущуюся вдоль эллиптической траектории, однако с видоизмененным параметрическим представлением: при t = а скорость камеры внезапно увеличивается в три раза. Такое движение описывается следующим уравнением:

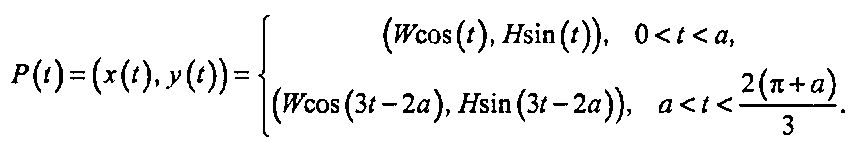
(11.4)

Такая ситуация показана на рис. 11.3. Сама траектория по-прежнему эллиптическая, однако при с = а л:(г) и г/(г) одновременно начинают колебаться в три раза быстрее, вследствие чего их производные при £ = а претерпевают разрыв. Это выглядит так, как если бы временные оси с этого момента были внезапно сжаты в три раза.

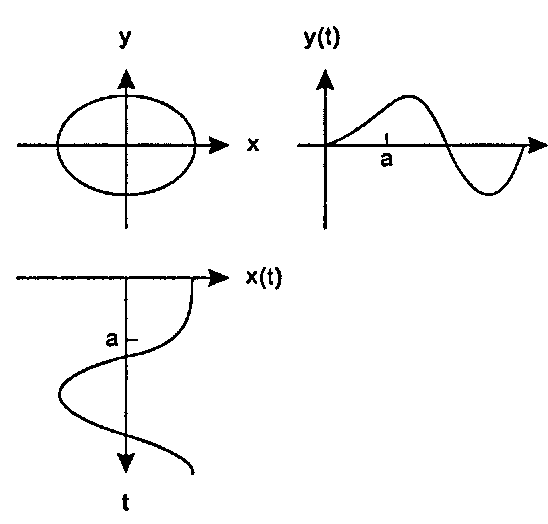
Рис. 11.3. Траектория движения с внезапным изменением скорости

11.1. Введение Векторы скорости в моменты с = а- («непосредственно перед» t = а) и t = а+ («сразу после» г = а) соответственно равны

Р'(а-) - (-Wsin(a), Hcos(a))

и (11.5)

Р'(а+) - (3Wsin(a), 3#cos(a)), так что направление скорости до и после изменения одинаково, однако величина скорости (длина вектора v(t)) внезапно скачкообразно увеличивается в три раза. На параметрическую кривую этот прыжок не влияет, однако характер движения точки P(t) вдоль этой кривой до и после момента t = а изменяется радикальным образом.

При изучении гладкости кривых и движения камеры полезно иметь величину, описывающую различные типы непрерывности, связанные с производными кривой. Мы будем изучать два вида гладкости, часто называемые параметрической непрерывностью (parametric continuity) и геометрической непрерывностью (geometric continuity).

Параметрическая непрерывность (С-непрерывность или к-непрерывность)

Говорят, что кривая Р(г) обладает параметрической непрерывностью k-io порядка всюду в интервале времени te [а, Ь], если все производные этой кривой, до k-ii включительно, существуют и непрерывны во всех точках внутри интервала [а, Ь]. Кратко это записывается так"opengl1_758.html">⇐ Предыдущая| |Следующая ⇒