Пусть, например, мы закрашиваем полигон, изображенный на рис. 10.34, и достигли строки развертки у = 50. Эта строка развертки пересекает четыре ребра полигона. Абсциссы этих пересечений, как легко вычислить, равны в порядке возрастания 45, 56,66, 70, 100. В таком случае закрашиваются два интервала от 45 до 56 и от 70 до 99.
10.7. Заполнение полигонально-определенных областей
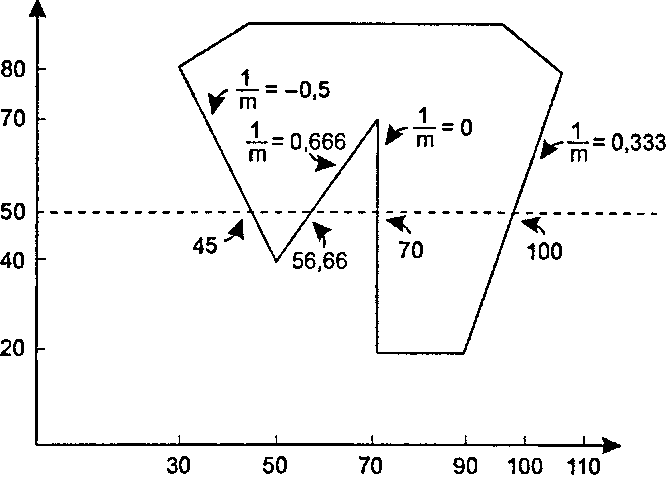
Рис. 10.34. Пример заполнения полигона Форма списка АЕЬ для такой ситуации предлагается на рис. 10.35, где показано четыре текущих пересечения, записанных по порядку, наряду с некоторыми другими данными, которые позволяют алгоритму быстро обновлять АЕЬ для использования в следующей строке развертки. Для каждого текущего пересекаемого ребра в списке АЕЬ содержатся следующие три элемента"images/tmp8E4A-701.png" alt="Список АЕ1. для строки развертки у = 50">
Рис. 10.35. Список АЕ1. для строки развертки у = 50
Второй элемент используется для определения мест пересечений следующей строки развертки у = 51 с каждым ребром. Отметим, что если наклон ребра равен т, то перемещение вверх на единицу приводит к увеличению абсциссы х пересечения на 1/т. (Проверьте это.) Значение 1/т непосредственно хранится в списке АЕЬ, как показано на рисунке. (К примеру, крайнее левое ребро простирается на 20 единиц по х и на 40 по у, так что обратная величина наклона составляет 20/40; проверьте остальные значения, приведенные на рисунке). Тогда при добавлении одного хы и 1/т определяется точка пересечения ребра со следующей (верхней) строкой развертки, в соответствии со свойством связности ребер.
Отметим, что именно добавление 1/т с последующим округлением и лежит в основе алгоритма Бре-зенхема для перемещения от точки к точке вдоль прямой. Фактически именно метод Брезенхема (заключающийся в приращении в зависимости от знака невязки с последующим обновлением этой невязки) наиболее предпочтителен в данной ситуации для достижения максимальной эффективности.
