В результате получаем такую последовательность значений (после выполнения команды 5ег.Р1хе1 (х.у)): х: 4 5 б 7 8 9 10 11 12 13 14 15 16 у: 112222333 3444 ?: -6 0 -18 -12 -6 0 -18 -12 -6 0 -18 -12 -6

На рис. 10.20 показано действие алгоритма на вышеприведенном примере, причем приводится как результирующая прямая, так и вариации функции ¥. На прямой ясно видны «ступеньки» в тех местах, где короткий горизонтальный отрезок терпит разрыв при переходе к следующему горизонтальному отрезку, на большей высоте.

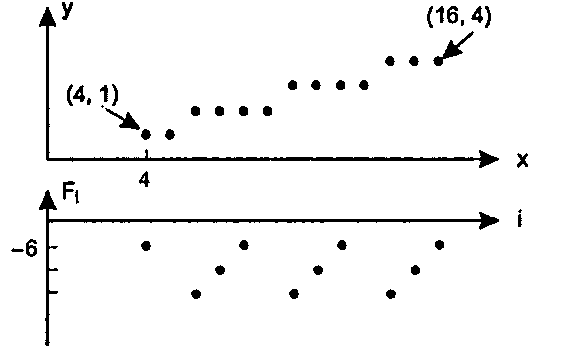
Рис. 10.20. Пример действия алгоритма средней точки Отмена ограничений на алгоритм Брезенхема Алгоритм Брезенхема применим только в частном случае, когда ах< Ьхи наклон прямой находится в диапазоне от нуля до единицы. Все остальные случаи также легко охватываются, если добавить код, обрабатывающий каждый случай более общего вида.

Получение той же прямой при ах > Ьх. Алгоритм средней точки определяет нахождение пиксела по нужную сторону от средней точки, выбирая на каждом шаге один из двух вариантов. Тогда нам нужно изменить код из листинга 10.5 так, чтобы он выполнял алгоритм средней точки для случая ах > Ьх. В действительности изменения требуются небольшие (см. упражнения в конце раздела). Следует отметить, что в рассматриваемом коде различаются два случая"opengl1_704.html">⇐ Предыдущая| |Следующая ⇒