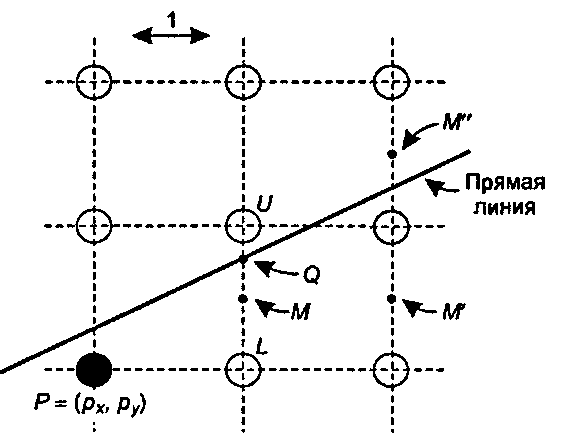
Рис. 10.19. Схема для вывода алгоритма средней точки Мы принимаем решение, включить пиксел и или Ь, в зависимости от того, лежит идеальная прямая выше или ниже средней точки М = (рх + 1, р + 1/2), расположенной посередине между точками и и Ь. Если мы вычислим функцию /"(,) в точке М, то ее знак укажет нам, проходит ли идеальная прямая выше или ниже точки М"images/tmp8E4A-682.png">
(10.7)Рассмотрим изменение функции /"(,) при переходе от х = рх + 1 к следующему значению х = рх + 2. Как показано на рис. 10.19, следующей средней точкой М будет либо точка М', либо точка М". Если мы не прибавили к у единицу на предыдущем шаге, то точкой М станет точка М' = (рх + 2,ру+ 1/2), а если прибавили, то точкой М станет точка М" = (рх + 2, ру + 3/2).
Случай 1. Если функция /"на предыдущем шаге была отрицательна (то есть значение у не изменялось), то
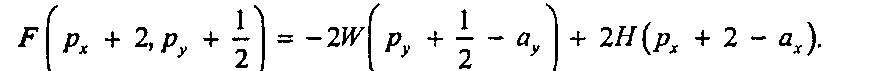
Вычтем из данного равенства равенство (10.7), чтобы определить, насколько последнее равенство больше, чем /"(М, М ):
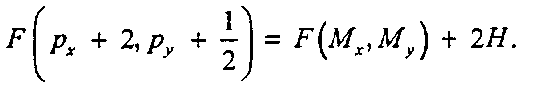
10.4. Рисование прямых своими силами: алгоритм Брезенхема Случай 2. Если функция Р на предыдущем шаге была положительна (то есть значение у было увеличено на 1), то
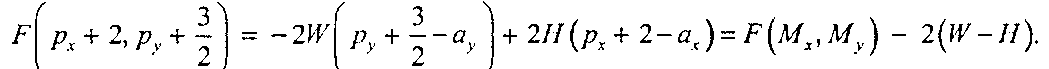
В каждом из случаев к «контрольной величине», то есть к исходному значению функции, добавляется некоторая константа: 2Н - если мы не увеличивали у, и -2( W- Н), если увеличивали.
Осталось определиться, с чего начинать этот процесс. Мы знаем, что при х = аху = а . Поэтому первый «экземпляр» средней точки М = (ах + 1, а + 1/2) и тогда
