Начнем с простого, однако крайне неэффективного метода, чтобы разъяснить основные идеи. Затем мы покажем значительно более быстрый метод, известный как алгоритм Брезенхема для рисования прямых линий (Bresenham's line-drawing algorithm).

21 Ф. Хилл

Средства для растровой графики

Предположим, что мы хотим задать значения пикселов так, что прямая появляется на экране между целыми координатами (ах, ау) и (Ьх, Ьу). На рис. 10.18 показано, какие пикселы «включаются» вдоль математически идеальной прямой между точками (ах, ау) и (Ьх, Ьу). Будем надеяться, что эти пикселы можно выбрать рационально и они в совокупности создадут впечатление прямой линии (хотя и с некоторыми неизбежными «ступеньками»).

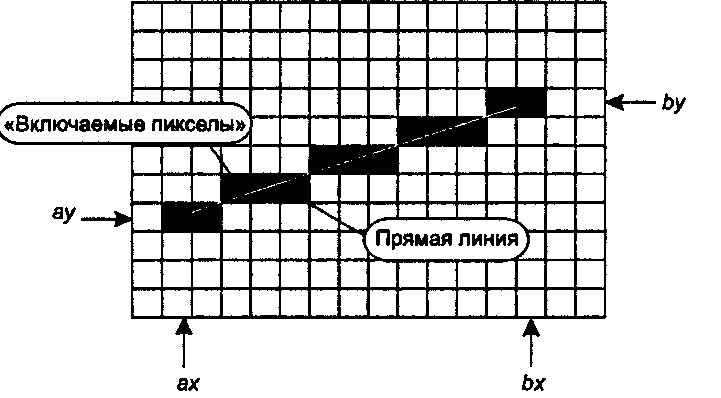
Рис 10.18. Рисование отрезка прямой линии Из элементарной алгебры известно, что прямая линия удовлетворяет уравнению ут(х- й ) + ау, где х изменяется от й до Ь, а величина

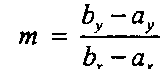
(10.3)
(10.4)

является наклоном (slope) этой прямой1. Если, например, дано (ах, ау) = (23,41) и (bx, Ьу) = (125, 96), то отсюда следует, что т ~ 55/102 - 0,5392. Наклон имеет смысл только для невертикальных прямых, у которых ах и Ъх различны. Для горизонтальной или вертикальной прямой очевидно, какие пикселы следует «включать», но для других прямых необходим алгоритм вычисления включаемых пикселов.

Простой, хотя и неэффективный метод заключается в том, чтобы двигаться по х от ах до Ьх с единичным шагом и на каждом шаге округлять соответствующее значение т(х - ах) + ау до ближайшего целого числа. В случае, когда ах меньше Ьх, этому методу соответствует следующий код"opengl1_699.html">⇐ Предыдущая| |Следующая ⇒