10.2.1. Конструирование буквы Я
Сконструируйте и нарисуйте двухуровневое изображение буквы Я размером 8 на 16 пикселов. Покажите сочетание единиц и нулей и картинку, которая получается, если 0 означает белый цвет, а 1 - черный.
10.2.2. Конструирование символов Сконструируйте красивые символы «а», «Л», «г», «/?», «?», «3» в пределах клеток из г строк и с столбцов. Выполните это для каждого из ниже перечисленных размеров клеток: О (г, с)-(6,4); О (г, с)-(10,8); О (г, с) = (14,12).
10.2.3. Слишком малы для узнавания?
Клетка размером (5,3) состоит из 15 пикселов и поэтому допускает 215 различных двухуровневых узоров из пикселов. Можно ли нарисовать в такой клетке все печатаемые АБСП-символы так, чтобы они были различными (и узнаваемыми)?
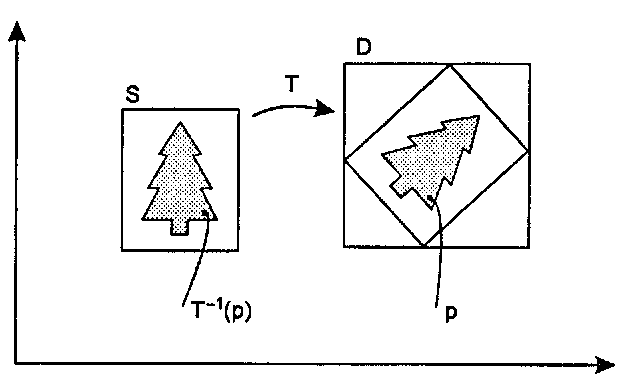
Рис. 10.9. Вычисление преобразованного изображения Практические упражнения
Средства для растровой графики
10.2.4. Уменьшение символов Один из методов уменьшения размера символа, заданного в виде прямоугольной пиксельной карты, состоит в сокращении в два раза длины клетки в обоих измерениях. Тогда каждый пиксел уменьшенной пиксельной карты должен имитировать то, что находилось в массиве пикселов размером 2 на 2 в исходной клетке. Разработайте алгоритм, который создает пиксельный узор размером (г, с) = (6,5) из пиксельной карты размером (г, с) = (12,10). Один из возможных способов формирования нового пиксела заключается в установке его в единицу, если два или более пикселов массива 2 на 2 равны единице. Хорош ли этот способ?
10.2.5. Поворот на 90° Рассмотрим квадратную пиксельную карту, представленную массивом A[i][j], где i и j изменяются от О до N-1. Выразите величину B[col][row] этой пиксельной карты, образованную поворотом А на 90° против часовой стрелки.
10.3. Объединение пиксельных карт
В определенных обстоятельствах бывает нужно объединить две пиксельные карты для получения из них третьей. Объединение пиксельных карт бывает полезным в таких ситуациях, как движение курсоров по экрану, сравнение двух изображений или морфинг (morphing), то есть плавная трансформация одного изображения в другое с помощью геометрических операций и цветовой интерполяции. Мы рассмотрим несколько примеров, имеющих практическое значение.
