Angle - 10 degrees.
Axiom - +WF--XF--YF--ZF.
W=YF++ZF----XF[-YF----WF]++.
X=+YF-ZF[--WF--XF]+.
Y=-WF++XF[+++YF++ZF]-.
Z--YF++++WF[+ZF++++XF]--XF.
F- empty

Для возможности автоматического изменения размеров окна, включающего каждую фигуру, приспособьте подпрограмму produceStringO так, чтобы при нулевом значении переменной visible рисование не производилось, а только вычислялись границы окна window = (w.l, w.t, w.r, w.b), полностью охватывающего обрабатываемую кривую. Если же visible - 1, то подпрограмма должна рисовать эту кривую. Для реализации этой схемы достаточно просто добавить к подпрограмме forwardO следующий тест: если visible - 0, то программа смотрит, вышло ли последнее значение CP (Current Position - текущих координат) за пределы окна, сформированного к этому моменту. Код для этого может выглядеть примерно так:

ifCCP.x < w.l) w.l - СР.х: if(СР.х > w.r) w.r - СР.х: etc.

// и так далее

Приближение к бесконечности

Как инициализируется такое окно?

Необязательное дополнение. Расширьте свое приложение так, чтобы оно могло рисовать фрактальные деревья, такие как «куст» на рис. 9.10.

Тематическое задание 9.2. Рисование снежинок и рептилий Уровень сложности II.

Часть А. Снежинка Мандельброта Мандельброт придумал замечательную самоподобную фрактальную кривую, которая в точности помещается внутри снежинки Коха (Koch snowflake). На обложке апрельского (1978) выпуска журнала Scientific American приведена кривая Мандельброта третьего порядка М3. Способ формирования кривой k-то порядка Мк основан на разбиениях равностороннего треугольника [Gardner, 78], как показано на рис. 9.51, а. Каждая из трех сторон равностороннего треугольника ABC разделена на три равные части точками от D до I.

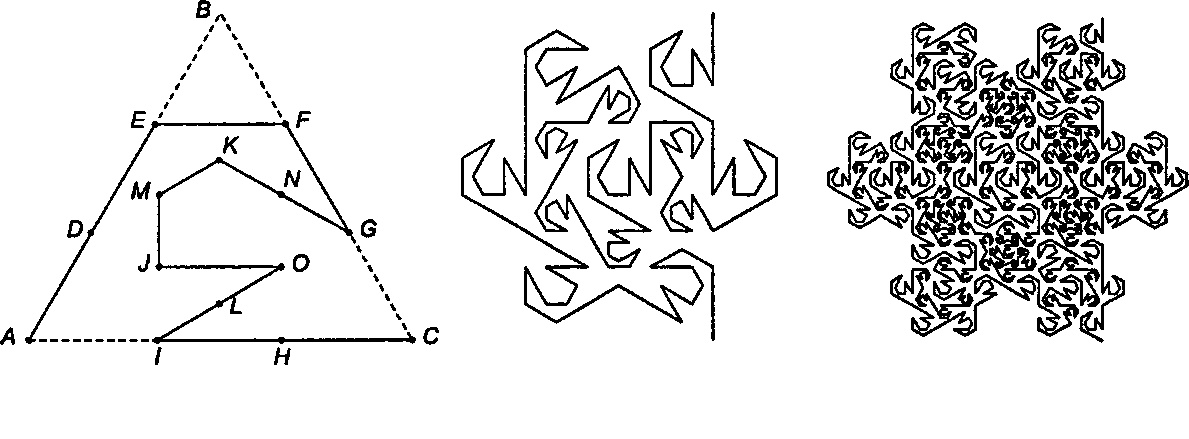
а б в Рис. 9.51. Построение снежинки Мандельброта Далее следующие отрезки также разделяются на три равные части: отрезок EG точками КиЫ, отрезок EI - точками М и/, а отрезок IG - точками L и О. Кривая Мандельброта первого порядка М, состоит из 13 отрезков ломаной линии ADEFGNKMJOLIHC. Эта кривая считается «построенной на отрезке» АС, причем она называется «левой», поскольку если смотреть из точки А на точку С, то кривая начинается с поворота влево. Для формирования снежинки следующего поколения Мг следует построить кривую такой же формы на каждом из 13 отрезков М,, как показано на рис. 9.51, б. Размер каждого отрезка определяет размер всей кривой. Некоторые из этих кривых являются левыми (I), а другие - правыми (R). Начиная с 5, последовательность поворотов выглядит так: RLLLLRRRLLRRL. Отметим, что кривая М2 размещается внутри снежинки Коха второго порядка. Напишите подпрограмму, которая рисует кривую Мандельброта М; для i = 1, 2,3. (На рис. 9.51, в показана кривая М3.)

⇐ Предыдущая| |Следующая ⇒