(F. F-F++F-F. nil. nil. 60)Квадратный остров Коха (Quadratic Koch Island):
(F+F+F+F. F+F-F-FF+F+F-F. nil. nil. 90)Кривая Гильберта (Hilbert curve)':
(X. F. -YF+XFX+FY-. +XF-YFY-FX+. 90)Кривая дракона (Dragon curve):
(X. F. X+YF+. -FX-Y. 90)Шестиугольная кривая Госпера (Gosper hexagonal curve):
( XF. F. X+YF++YF-FX--FXFX-YF+, -FX+YFYF++YF+FX- -FX - Y. 60)Ковер Серпинского (Sierpinski gasket): (FXF--FF--FF. FF. --FXF++FXF++FXF--. nil. 60) Наконечник Серпинского (Sierpinski arrowhead):
(YF. F. YF+XF+Y. XF-YF-X. 60)1 Эта кривая названа в честь великого математика Дэвида Гильберта (David Hilbert, 1862-1943).
9.3. Создание строк и кривые Пеано Здесь приводятся данные для семи классов кривых. Для каждой кривой задаются пять ключевых компонентов в следующем порядке: атом, F-строка, Х-строка, Y-строка, угол в градусах; словом <nil» (нуль) здесь обозначена пустая строка. Примеры четырех из этих кривых показаны на рис. 9.7.
Некоторые кривые, показанные на рис. 9.7, фактически являются кривыми, заполняющими плоскость (space-filling), или кривыми Пеано (Peano curves). Как уже упоминалось ранее, дробная размерность таких кривых равна 2, и они полностью заполняют определенную область плоскости. Две самые известные из них - это кривые Гильберта и Серпинского. (Позднее была открыта «снежинка» Ман-дельброта, рассматриваемая в тематическом задании 9.2.) На рис. 9.8 показано несколько кривых Гильберта низших порядков.
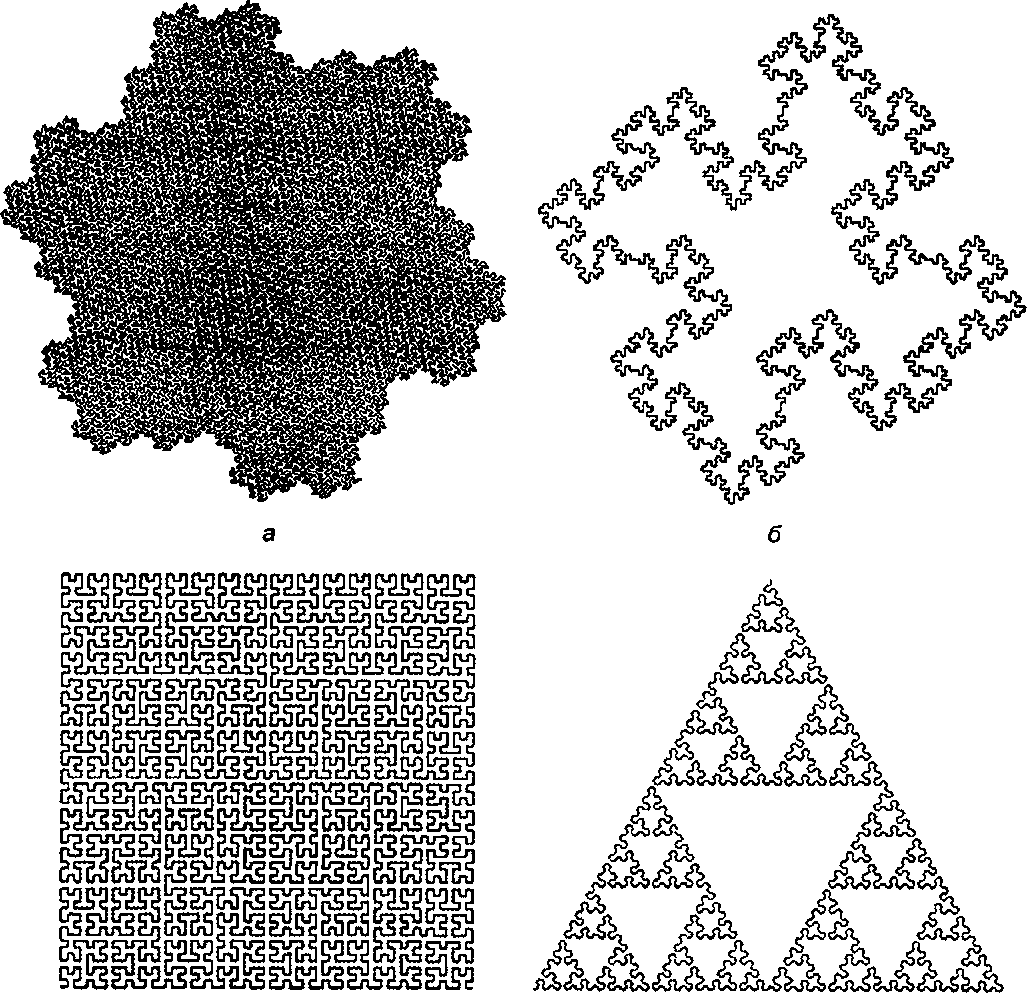
в S
Рис. 9.7. Примеры кривых, созданных с использованием инструкций генерирующих строк: а) кривая Госпера пятого порядка; б) квадратный остров Коха третьего порядка; в) кривая Гильберта (Hilbert) шестого порядка; г) наконечник Серпинского (Sierpinski) седьмого порядка Гильберт доказал, что при стремлении порядка к бесконечности бесконечно тонкая непрерывная кривая Гильберта проходит через каждую точку единичного квадрата! Кроме описанного здесь метода генерации строк, существуют другие способы рисования кривых Гильберта (см. [Wirth, 213] и [Griffith, 95]).
