1 Мы возвращаемся к обозначениям параметров и и с в параметрическом представлении формы, поскольку 5 и г заняты для текстурных координат.
Визуализация граней для усиления реалистичности
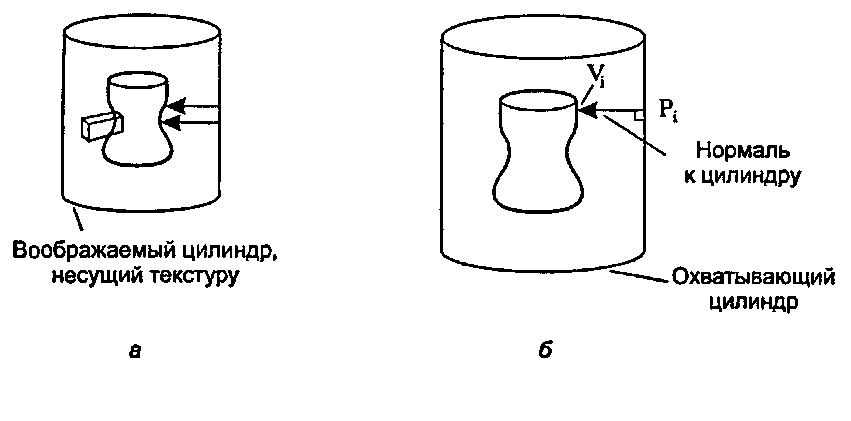
Рис. 8.52. Обертывание со сжатием текстуры на вазу Бир и Слоун предлагают некоторые альтернативные способы связывания точек текстуры на воображаемом цилиндре с вершинами объекта. На рис. 8.53 показаны две такие возможности. На рис. 8.53, а проводится прямая из центра тяжести объекта С через вершину У( до ее пересечения с цилиндром в точке Р.. На рис. 8.53, б используется нормальный вектор к поверхности объекта в точке V:. Р{ является точкой пересечения этой нормали из точки У{ с цилиндром. Отметим, что три вышеприведенных способа связывания точек текстуры с точками объекта могут привести к весьма различным результатам, зависящим от формы объекта (см. упражнения в конце раздела). Разработчику следует выбрать наиболее подходящий метод, исходя из формы объекта и характера отображаемого текстурного изображения. (Какой из этих методов подошел бы для шахматной пешки?)
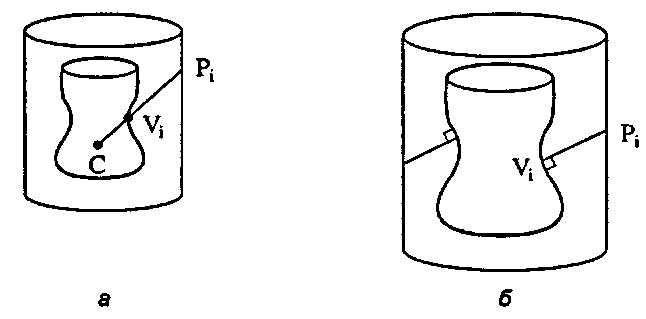
Рис. 8.53. Альтернативные отображения с воображаемого цилиндра на объект Пример 8.5.3. Отображение текстуры на сферу С точки зрения топологии вокруг цилиндра легко обернуть текстурный прямоугольник: цилиндр можно разрезать и развернуть на плоскости без искажения. Иначе обстоит дело со сферой: как известно всем картографам, не существует способа показать точные детали всего глобуса на плоском листе бумаги. При разрезании сферы и ее распрямлении некоторые части всегда подвергаются существенному растяжению. (Попытайтесь представить себе шахматную доску, обернутую вокруг всей сферы!)
В то же время нетрудно наклеить прямоугольную текстуру на часть сферы. Для того чтобы отобразить текстурный квадрат на часть сферы, лежащую между углами от 8а до дь по долготе (азимуту) и от фа до фь по широте, просто выполним линейное отображение согласно уравнению (8.22). Если координаты вершины V, равны (8., ф), то мы свяжем их с текстурными координатами
