Изначально массив d[ ][ ] заполняется значениями 1,0, что соответствует максимально возможной псевдоглубине. Буфер кадров изначально заполняется цветом фона.

Нахождение псевдоглубины для каждого пиксела Нам необходимо найти быстрый способ вычисления псевдоглубины для каждого пиксела. Напомним, что каждая вершина Р - (Рх, Ру, Рг) любой грани пересылается в графический конвейер и подвергается там различным преобразованиям. Информация, доступная для каждой вершины после преобразования порта просмотра, представляет собой значение упорядоченной тройки, которая после масштабирования и сдвига определяется формулой:

Визуализация граней для усиления реалистичности

(См. также равенство (7.11).) Третий компонент этой тройки и есть псевдоглубина. Константы а и Ь выбраны так, чтобы третий компонент обращался в нуль, если вершина Р лежит на ближней плоскости, и в единицу, если Р лежит на дальней плоскости. Для большей эффективности псевдоглубину каждого пиксела желательно вычислять в приращениях (инкрементно), что предполагает использование линей- * ной интерполяции, как это делалось для цвета в равенстве (8.14).

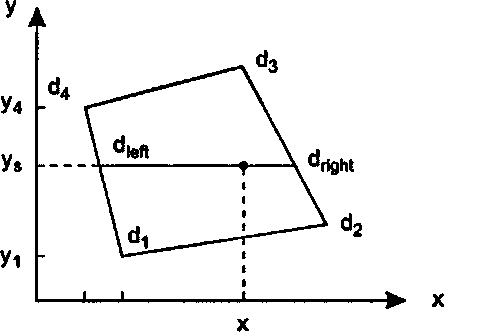
Рис 8.29. Инкрементное вычисление псевдоглубины

На рис. 8.29 изображена грань, закрашиваемая вдоль строки развертки у. На рисунке отмечены значения псевдоглубины в различных точках. Известны псевдоглубины dv d2, d3, d4 для вершин. Нам требуется вычислить dlck для строки развертки ys как 1егр(^,, dvf) для части f~(y,- г/,)/(г/4 - г/,) и аналогично d^ как \erp(d2, d3, А) для соответствующего А. Кроме того, нам нужно найти псевдоглубину адля каждого пиксела (х, у) вдоль строки развертки как lerp(dkk, ^right, k) для соответствующего k. (Чему равны значения А и k?) Вопрос заключается в том, получается ли в результате этих вычислений «истинная» псевдоглубина соответствующей точки на трехмерной грани. Ответ на этот вопрос будет положительным"opengl1_554.html">⇐ Предыдущая| |Следующая ⇒