15 Ф. Хилл
Трехмерный просмотр
фективнее выбрать функцию с тем же знаменателем (-Р2), что и у величин х* и у*. Итак, возьмем функцию с таким знаменателем и числителем, пропорциональным Р., тогда точка Р «проецируется» в точку
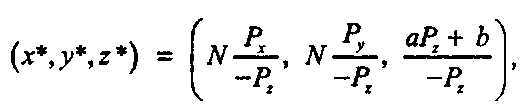
где а и Ъ - некоторые константы. Хотя подошли бы многие другие значения а и 6, мы выберем их так, чтобы псевдоглубина изменялась в пределах от -1 до 1. (Позже мы увидим, почему такой выбор является удачным.). Так как глубина увеличивается по мере того, как точка перемещается дальше вдоль отрицательной оси г, мы назначаем псевдоглубину равной -1 при Рг = -ЛГ и +1 при Рг - -Р. Имея два этих условия, легко вычислить а и Ъ:
(7.8)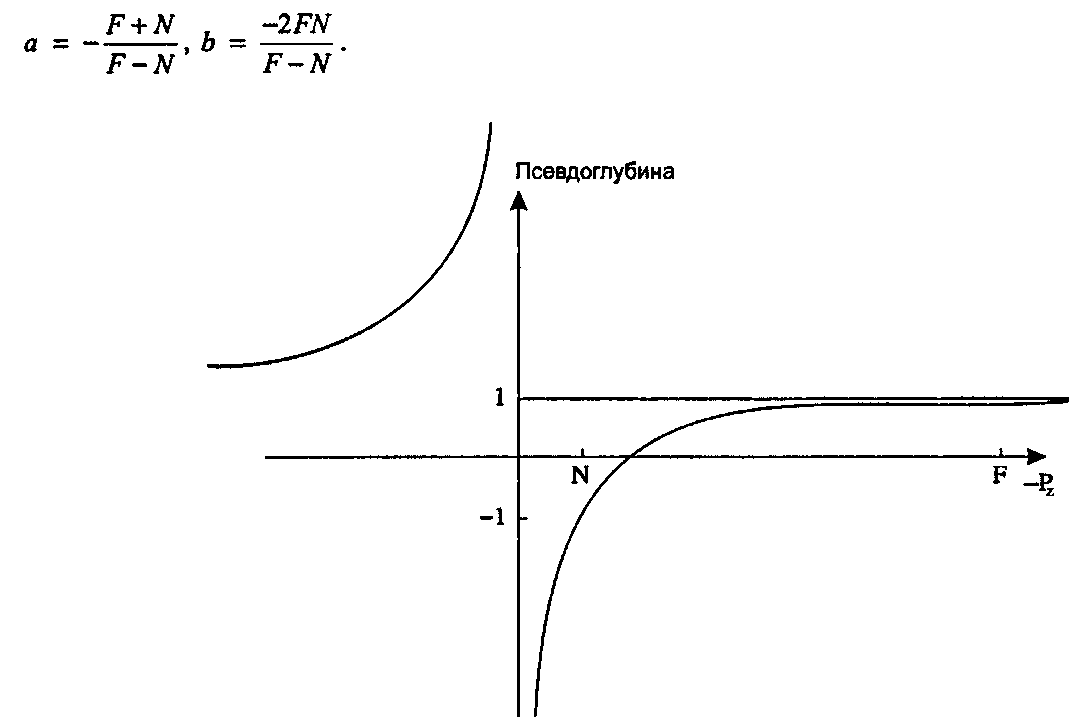
Рис. 7.24. Псевдоглубина растет по мере роста модуля отрицательных значений Рг На рис. 7.24 начерчен график зависимости псевдоглубины от (-Р ). Как мы уже установили, она растет от -1 для точки на ближней плоскости до 1 для точки на дальней плоскости. Когда Рг приближается к нулю (так что точка находится прямо перед глазом), псевдоглубина стремится к минус бесконечности. Для точки, находящейся непосредственно позади глаза, псевдоглубина большая и положительная. Однако мы будем отсекать точки, располагающиеся ближе ближней плоскости, поэтому такое катастрофическое поведение нам никогда не встретится.
Отметим, что значения псевдоглубины сгущаются по мере того, как -Рг становится ближе к £ В силу конечной точности компьютерной арифметики такое сгущение может вызвать проблему, например, при удалении невидимых поверхностей, когда нужно будет различить псевдоглубины двух точек. Фактические глубины точек относительно глаза могут быть различны, однако их псевдоглубины окажутся одинаковыми!
Отметим, что определение псевдоглубины согласно уравнению (7.7) приводит к росту ее положительных значений по мере роста отрицательных значений Рг. Такое поведение представляется естественным, поскольку расстояние от глаза растет по мере того, как Р2 перемещается дальше вдоль отрицательной оси 2.
7.4. Перспективные проекции трехмерных объектов
