В заключение посмотрим, какие величины функция gluLookAtO заносит в матрицу моделирования-вида. Из главы 5 мы знаем, что матрица моделирования-вида является произведением двух матриц: матрицы У, ответственной за преобразование точек из мировых координат в координаты камеры, и матрицы М, осуществляющей все преобразования моделирования, применяемые к этим точкам. Функция gluLookAtO строит матрицу У и умножает ее справа на текущую матрицу. Поскольку задача матрицы У заключается в преобразовании мировых координат в координаты камеры, она должна преобразовывать систему координат камеры в исходную позицию камеры, как показано на рис. 7.9. Это означает, что матрица У должна преобразовать точку eye в начало координат, вектор и в вектор i, v в j, п в к. Имеется несколько способов получения матрицы У, однако проще убедиться, что подойдет такая матрица:
V =(их иу иг dx\
vx vy vz dy
nx ny nz dz
0 0 0 0
(7.2)7.2. Снова о камере
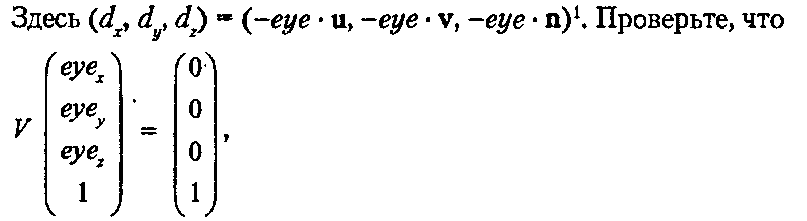
как и должно быть, где точка eye расширена до однородных координат. Проверьте также, что
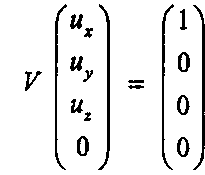
и что матрица ^преобразует вектор V в (0,1,0,0)7", а вектор п - в (0,0,1,0)г. Матрица ^создается функцией д!и1.оокАт.() и умножает ее справа на текущую матрицу. У нас будет возможность произвести такую операцию позднее, когда мы встроим в программу нашу собственную камеру.
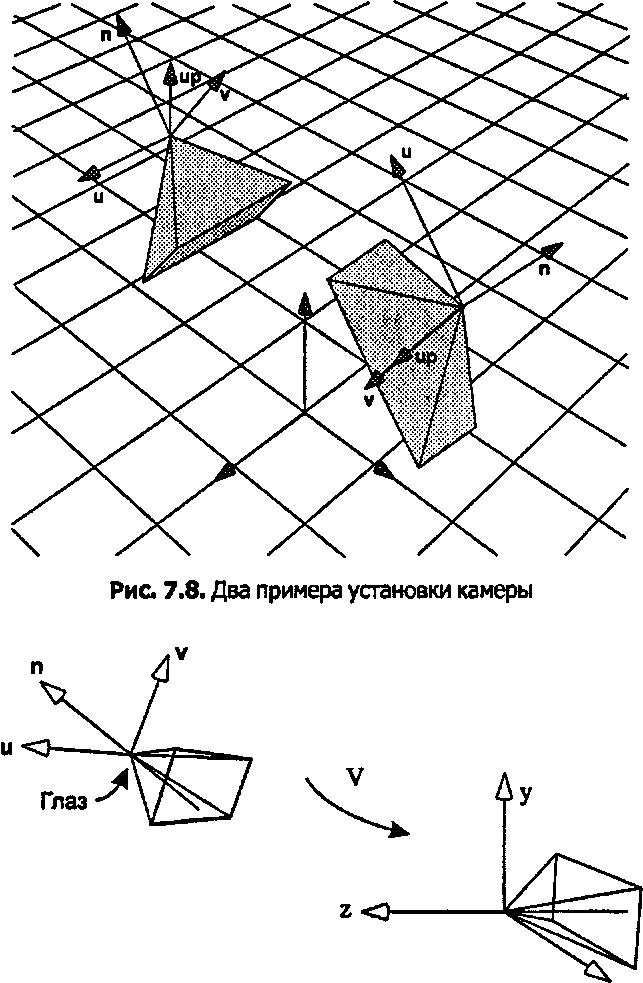
XРис. 7.9. Преобразования, осуществляемые функцией gluLookAtQ
1 Ввиду того, что нельзя скалярно перемножать точку и вектор, вместо точки eye нужно взять вектор eye - (0,0,0).
Трехмерный просмотр
Практические упражнения
7.2.1. Нахождение крена, тангажа и курса по заданным векторам и, V, п Пусть камера задана системой координат, образованной ортами и, V, п. Курс и тангаж камеры определяются путем выражения вектора -п в сферических координатах. Используя приложение Б, покажите, что курс = агсг£(-я,, -пх), тангаж = виг^-я ).
Далее, крен камеры - это угол между осью и и горизонтом. Для определения крена построим горизонтальный вектор Ь, лежащий в плоскости иь. Покажите, что Ь = j х п удовлетворяет этим требованиям. Кроме того, покажите, что угол между векторами Ь и и определяется формулой:
