Моделирование поверхностей полигональными сетками
Можно также производить чисто геометрические деформации [Barr, 13], которые дизайнеры применяют для визуального эффекта. Например, нетрудно изменять поперечное сечение (taper) объекта вдоль оси, как показано на рис. 6.76. Это достигается масштабированием всех точек в направлениях х и у на величины, зависящие от z, в соответствии с некоторой профильной функцией, например g(z). Такая функция определяет (неаффинное) преобразование, которое можно записать в форме матрицы масштабирования
(6.54)Если поверхность до преобразования имеет параметрическое представление Р(и, v) - (Х(и, v), Y(u, v), Z(u, v)), то его деформация, заданная равенством (6.54), преобразует его в форму:
F(u, V) - (Х(и, V) g(Z(u, V)), Y(u, v) g(Z(u, v)), Z(u, v)). (6.55)
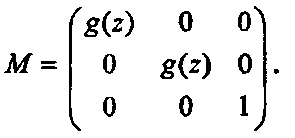
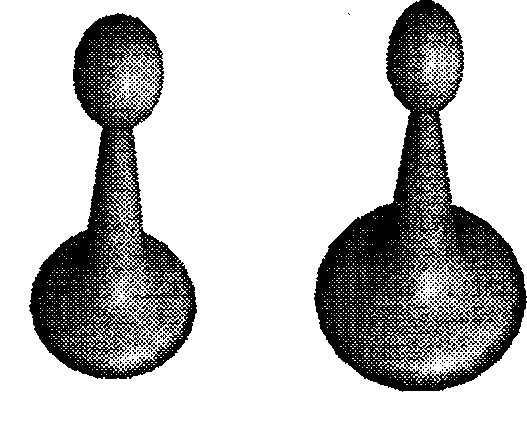
Рис. 6.76. Пешка до и после суживания Для того чтобы получить рис. 6.76, вначале была создана сетка для пешки, затем каждая вершина этой сетки (лг, у, z) была преобразована в (xF, yF, z), где функция F - 1 - 0,04(z + 6). (Отметим, что эта пешка простирается по оси 2 от 0 до -12.)
Еще одним полезным видом деформации является закручивание (twisting). Например, для закручивания объекта вокруг оси z нужно повернуть все точки объекта вокруг этой оси на угол, зависящий от z, используя матрицу"images/tmp8E4A-450.png">
(6.56)На рис. 6.77 показана пешка после того, как к ней было применено линейно возрастающее закручивание. Пешка является поверхностью вращения вокруг оси z, поэтому нет особого смысла закручивать ее относительно этой оси. Вместо этого закручивание здесь производилось вокруг оси# с помощью функции g(z) = 0,027t |z + 6|.
Примените эти деформации к нескольким каркасным моделям, в том числе к тору. Имейте в виду, что ни для одной из деформаций вам не удастся использовать матрицу моделирования-вида OpenGL, поскольку преобразования в данном случае не являются аффинными. Нужно преобразовывать вершины из текущего списка вершин. Изгиб (bending) - это еще одна деформация, примененная Барром. Обратитесь к его работе [Barr, 13] и поэкспериментируйте с деформацией изгиба.
