8. Покажите, что площадь этой трапеции равна произведению длины ее основания на высоту средней точки ребра. Например, площадь Ай на рисунке равна Ай = 0,5(х0 -xi)(y0 + г/,). Эта величина отрицательна, если х0 лежит левее xt, и положительна в противном случае. Применим эту формулу к остальным ребрам. Тогда для i-ro ребра имеем:
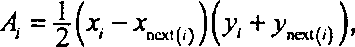
где next(i) равно 0 при i = N- 1 и равно i + 1 в остальных случаях.
Моделирование поверхностей полигональными сетками
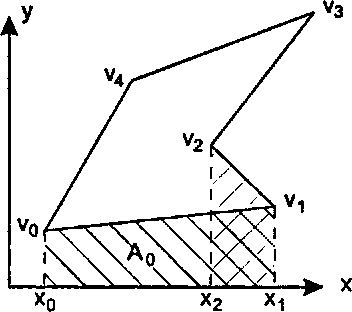
Рис. 6.69. Вычисление площади полигона
9. Докажите, что если два смежных ребра полигона коллинеарны (что обратит их векторное произведение в нуль), то площадь, находящаяся между этими ребрами, по-прежнему вычисляется правильно.
10. Докажите, что А. равно либо площади полигона, либо этой площади со знаком минус.
Теперь рассмотрим вопрос, какое из двух основных направлений вектора т указывает вовнутрь. Иначе говоря, если вы поворачиваете пальцы правой руки вокруг вершин полигона, двигаясь от Р0 к Р{, затем к Р2 и т. д. (то есть в направлении стрелки на рис. 6.70), то куда указывает вектор т - вдоль вашего большого пальца или в противоположном направлении?
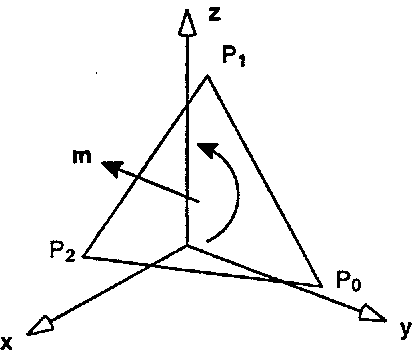
Рис. 6.70. Направление нормали, найденной по методу Ньюэлла
11. Докажите, что вектор m действительно направлен так, как показано на рис. 6.70. Таким образом, для сетки, у которой внешняя и внутренняя стороны четко определены, можно утверждать, что вектор m является «внешней» нормалью, при условии, что вершины пронумерованы против часовой стрелки, если смотреть снаружи.
Тематическое задание 6.3. Призма Уровень сложности III.
Напишите приложение, позволяющее пользователю задавать полигональное основание призмы с помощью мыши. Затем эта программа должна создавать списки вершин, нормалей и граней для этой призмы и отображать последнюю на дисплее.
Рисунок 6.71, а показывает «область рисования» пользователя - прямоугольник на экране. Пользователь задает мышью последовательность точек внутри этого прямоугольника, прерывая этот процесс нажатием правой кнопки мыши.
