Моделирование поверхностей полигональными сетками

Напишите приложение, которое читает каркасные объекты из файлов и рисует эти объекты. Пусть эта программа позволяет пользователю записывать каркасный объект в файл. Начните работу своего приложения с создания сеток для тетраэдра и простого сарая.

Тематическое задание 6.2. Вывод метода Ньюэлла Уровень сложности И.

В этом задании излагается теория, на которой основан метод Ньюэлла (Newell method), предназначенный для вычисления нормалей к полигону, заданному своими вершинами. По ходу изложения про-делываются необходимые математические выкладки. Вы должны получить несколько промежуточных результатов. Мы будем работать с полигональной гранью

P-{?vPt.....Рк-г)> (6.50)

заданной своими N трехмерными вершинами. Мы хотим показать, почему формулы в равенстве (6.1) обеспечивают точное вычисление нормального вектора m = (тх, т , тг) к грани Р в случае, когда Р является плоской; и предлагают хорошее направление для «усредненной» нормали, когда Р - неплоская грань.

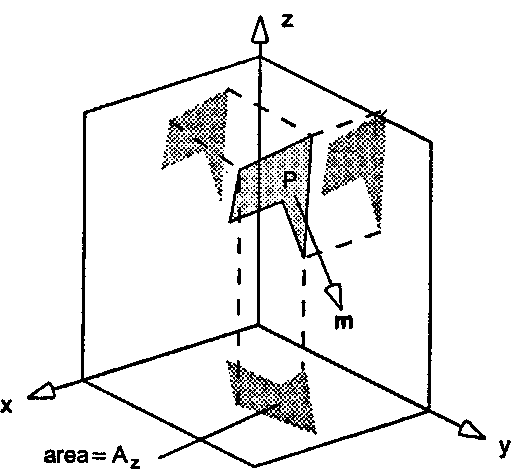
Рис. 6.67. Использование спроецированных областей для нахождения нормального вектора А. Вначале рассмотрим рис. 6.67, на котором показана грань Р, ортогонально (то есть вдоль главных осей) спроецированная на каждую из главных плоскостей, а именно на плоскости х = 0, у = 0, z = 0. Каждая проекция является двумерным полигоном. Прежде всего покажем, что компоненты вектора m пропорциональны соответственно площадям Ах, Ау, Аг этих спроецированных полигонов. Для простоты рассмотрим случай, когда Р является треугольником, как показано на рис. 6.68. Обозначим этот треугольник Т, а его единичный нормальный вектор - т. Пусть, далее, Ґ является проекцией треугольника Т на плоскость с единичной нормалью п. Покажем, что площадь Ґ, обозначенная Агеа(Г'), является определенной частью от площади всего треугольника Т, обозначенной Агеа(Т), и что эта часть является скалярным произведением"opengl1_447.html">⇐ Предыдущая| |Следующая ⇒