6.5. Каркасные аппроксимации гладких объектов

галерея художественная ковка дачные столы стулья скамейки.

6.5.4. Три «базовые» формы: сфера, цилиндр и конус

В этом разделе мы начнем с трех классических объектов - «базовых» («generic») версий сферы, цилиндра и конуса. Для каждого из этих объектов рассматриваются его неявная и параметрическая форма, а также способы создания сеток для их аппроксимации. Мы выведем формулы для определения нормального направления в каждой точке данного объекта. Отметим, что в главе 5 для рисования таких форм уже использовались функции OpenGL. Однако добавление своих собственных инструментов имеет два преимущества: во-первых, мы достигаем значительно более строгого контроля за деталями структуры создаваемой формы, а во-вторых, мы фактически получаем объект в виде сетки и можем применять к нему методы класса Mesh.

Базовая сфера Назовем сферу единичного радиуса с центром в начале координат «базовой сферой» (см. рис. 6.46, а). Она является основой для всех остальных используемых нами сфероподобных форм. Неявная форма для такой сферы хорошо известна:

F(x,y,z) = x2 + y2 + z2- 1. (6.28)

При альтернативном способе записи F(Р) мы получаем более элегантное выражение: F(P) = \Р\2 - 1. (Как изменятся эти формулы, если радиус сферы будет равен R?)

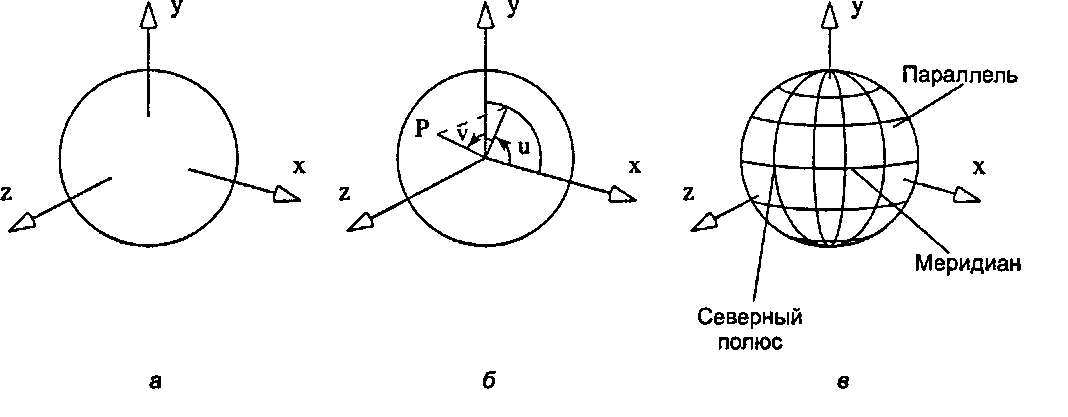
Рис. 6.46. Базовая сфера (я); параметрическая форма (5); параллели и меридианы (а)

Параметрическое описание этой сферы непосредственно вытекает из стандартного описания точки в сферических координатах (см. приложение Б.) Пусть величина и соответствует долготе (азимуту), a v - широте. Тогда произвольная точка на сфере Р = (х, у, z) выражается в сферических координатах как (cos (v) cos (и), cos (v) sin (и), sin (г>)) (см. рис. 6.46, б). Для того чтобы охватить все точки на сфере, и должно изменяться в диапазоне (0,2л), a v - в диапазоне (-л/2, л/2)1. Поэтому параметрическая форма сферы имеет вид"opengl1_422.html">⇐ Предыдущая| |Следующая ⇒