'0,7 0 0 04
0 0,7 0 0м =
0 0 1 Я
,° 0 0 К
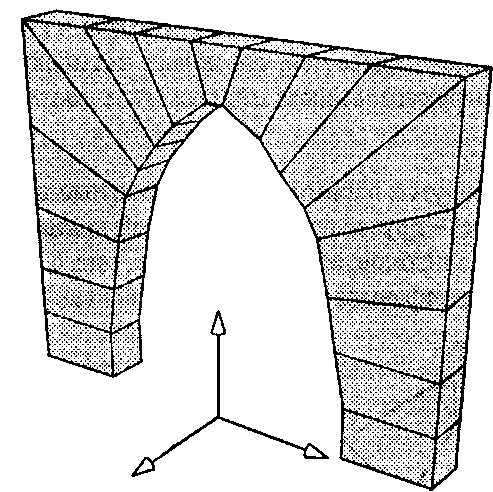
Рис. 6.33. Экструзивная полоса четырехугольников, образующая арку
Эта матрица содержит только масштабный множитель 0,7 и перемещение на Я единиц вдоль оси г. На рис. 6.34, в показан конический цилиндр, крышка которого перед перемещением была повернута вокруг оси 2 на угол 9. Такое преобразование описывается матрицей"images/tmp8E4A-392.png">
Рисунок 6.34, г демонстрирует в разрезе, как повернуть крышку Р' на нужный угол перед ее перемещением в желаемую позицию.
Призмы, подобные этим, столь же просто создавать, как и те, для которых в матрице М используется только перемещение: список граней для такой призмы тот же, что и у исходной; изменяются только координаты вершин и значения нормальных векторов.
6.4. Экструзивные формы
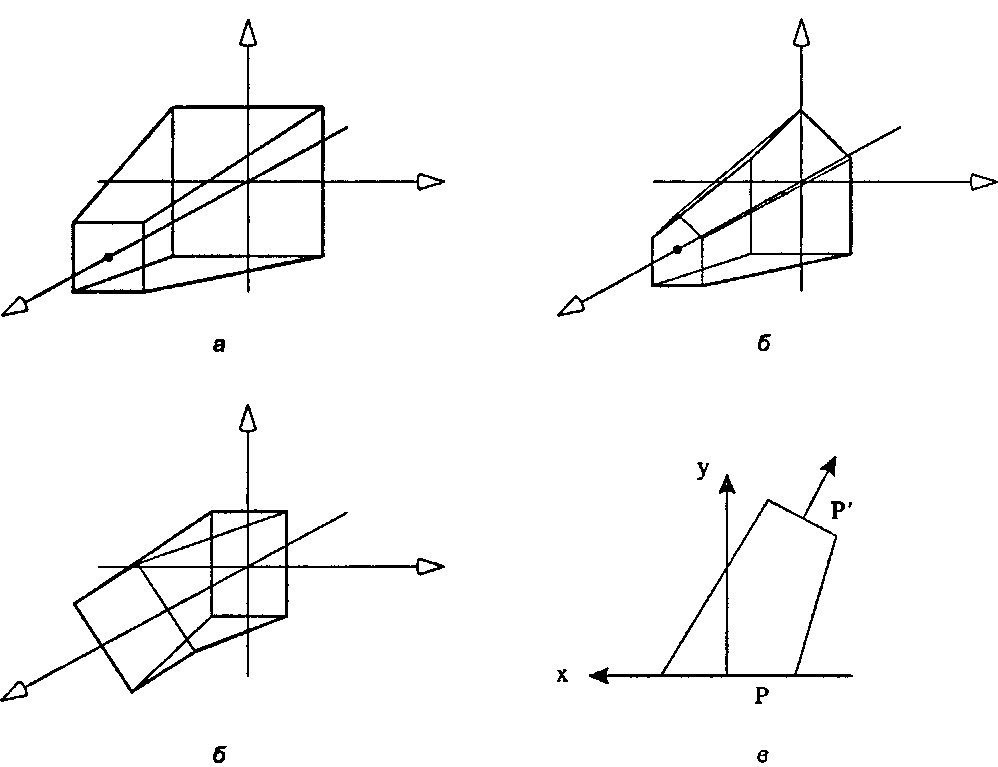
Рис. 6.34. Пирамиды и повернутые призмы
Практические упражнения
6.4.1. Конический цилиндр
Составьте детальное описание того, как составить списки вершин, нормалей и граней для усеченной пирамиды, основания которой представляют собой правильные пентагоны, причем верхнее основание в два раза меньше нижнего.
6.4.2. Тетраэдр как усеченный конус
Опишите моделирование тетраэдра как конического цилиндра с треугольным основанием. Является ли этот способ эффективным при вычислении сетки для тетраэдра?
6.4.3. Антипризма Обдумайте, как создать антипризму, изображенную на рис. 6.15, б. Можно ли ее смоделировать как вид экструзии?
6.4.4. Создание сегментированных экструзий"opengl1_409.html">⇐ Предыдущая| |Следующая ⇒
