Этот класс шире класса движений жесткой конструкции, поскольку он включает в себя равномерное масштабирование. Он также является важным классом, поскольку, как мы увидим в главе 8, вычисления освещенности и затенения зависят от скалярных произведений различных векторов. Если данное преобразование не изменяет углы, то оно не изменяет и скалярные произведения, и в этом случае вычисления освещенности можно осуществлять как в преобразованном, так и в непреобразованном пространстве.
Преобразования объектов
Разложение трехмерного аффинного преобразования. Для заданного трехмерного аффинного преобразования {Л/, d} мы хотим знать, из какой последовательности элементарных преобразований оно составлено. Проделаем вслед за Голдманом [Goldman, 83] все шаги, требующиеся для разложения матрицы М размерностью три на три в произведение масштабирования 5, поворота R и двух сдвигов Я, и Я2 (уравнение (5.51)).
Вам предлагается проверить каждый шаг на этом пути и разработать подпрограмму, создающую матрицы 5, R, Я, и Я2 по отдельности.
Пусть имеется матрица М со строками u, v, w, каждая из которых представляет собой трехмерный вектор:
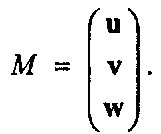
Подход Голдмана основывается на классической процедуре ортогонализации Грама-Шмидта (Gram-Schmidt), посредством которой строки матрицы М комбинируются таким образом, что они становятся взаимно ортогональными и имеющими единичную длину. Следовательно, матрица, состоящая из таких строк, является ортогональной и поэтому представляет вращение (или вращение с отражением). Голдман показал, что процесс ортогонализации по существу представляет собой два сдвига. Остальное - уже детали. Тщательно выполните каждый из следующих шагов (по Голдману), а также все задания, заключенные в круглые скобки.
1. Нормируйте вектор и в u* ** и/5,, где 5, -,|и|.
2. Вычтите часть вектора и* из вектора v так, чтобы остаток был ортогонален и*. Пусть b - v - du*, где d - v и*. (Покажите, что b и* - 0.)
3. Нормируйте вектор Ь, для чего задайте вектор v* = b/S2, где 52 - |Ь|. _
