Это довольно общий результат, показывающий, как повернутая точка Q может быть разложена на части вдоль вектора h и вдоль двух ортогональных осей, лежащих в плоскости вращения.
В представлении точки Q, приведенном в уравнении (5.48), с трудом можно узнать произведение точки Р на некоторую матрицу, однако это так, поскольку каждый из трех слагаемых пропорционален вектору р. Преобразуем каждый из членов этого уравнения в нужную нам форму следующим образом: в) Заменим вектор р на Р, откуда сразу получим p(cosß) - /(cosß)P, где /- единичная матрица размерностью три на три.
документы для водителя на контракт.
г) Используем тот факт (см. приложение Б), что скалярное произведение двух векторов р и может быть записано в форме произведения точки Р на матрицу: (птР) и покажем, что (р u)u - итиР, где uru - тензорное произведение, аналогичное приведенному в равенстве (5.46).
д) Используем утверждение из приложения Б, что векторное произведение двух векторов и х р может быть также записано в форме произведения Р на некоторую матрицу, и покажем, что u х р - Cross (u)jP, где матрица Cross(u) имеет следующий вид:
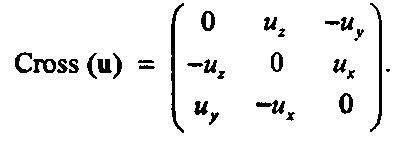
(5.49)е) Собирая эти члены вместе, получим матрицу1
М - совр / + (1 - соэр) иги + втр Сгозз(и), (5.50)
следовательно, М является суммой трех взвешенных матриц, что, несомненно, проще построить, чем произведение пяти матриц, как это было при классическом выводе.
ж) Выведите равенство (5.33) из равенства (5.50).
1 В работе Голдмана [Goldman, 83] приводится та же форма для матрицы Ми даются компактные результаты для нескольких других сложных преобразований.
5.8. Тематические задания Тематическое задание 5.6. Разложение трехмерных аффинных преобразований Уровень сложности III.
В данном тематическом задании рассматривается несколько обширных семейств аффинных преобразований.
Что такое трехмерное аффинное преобразование?
Мы вновь игнорируем связанную с перемещением часть аффинного преобразования и сосредоточимся на той его линейной части, которая представлена матрицей М размерностью три на три. Что же за преобразование «вложено» в М? Голдман [Goldman, 83] показал, что каждая такая матрица Мявляется произведением масштабирования 5, поворота R и двух сдвигов Я, и Я2, а именно:
