Г.
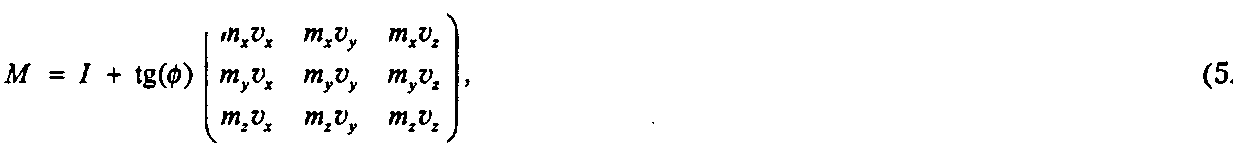
где / - единичная матрица размерностью три на три. Некоторые детали вывода уравнения (5.44) приводятся ниже.
Пример 5.8.2
Найдите сдвиг, соответствующий плоскости, имеющей единичную нормаль ш = (1,1,1)/л/з - (0,577, 0,577, 0,577), единичному вектору V - (0,0,707, -0,707) и углу 0-30°. Решение Заметим, что вектор V, как и требуется, лежит в данной плоскости. (Почему?) Используя равенство (5.44), получим:
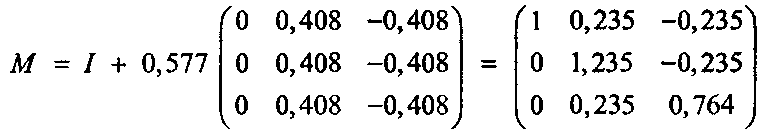
5.8. Тематические задания
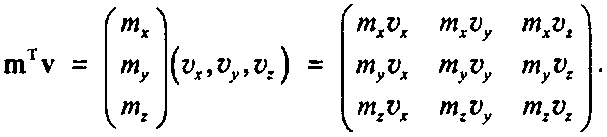
Выведем теперь матрицу сдвига. Мы хотим выразить точку () с рис. 5.60 через точку Р и «компоненты» сдвига. Расстояние (с учетом знака) от точки Рдо плоскости определяется выражением Р т (если рассматривать точку Р как радиус-вектор, исходящий из начала координат). Собирая вместе все компоненты, получим:
<2-Р+(Р-тШ0)у. (5.45)
Отметим, что точки «по другую сторону плоскости» сдвигаются в противоположном направлении, как и ожидалось.
Теперь нам требуется найти второй член, представляющий собой произведение Р на некоторую матрицу. Известно, что Р т = РтТ (см. приложение Б), откуда 0_ = Р(1 + Щ(ф) тту). Теперь покажем, что матрица сдвига равна (/+ tg(0) тту), где член шту имеет следующий вид:
(5.46)Это выражение носит название внешнего произведения (outer product) или тензорного произведения (tensor product) вектора m на вектор v.
Практические упражнения
5.8.9. Связь с простым сдвигом Напишите выражение для сдвига, определяемого направлением v = (1, 0, 0) и плоскостью, имеющей нормальный вектор (0, 1, 0). Докажите, что для любого угла фэю выражение совпадает с элементарной матрицей сдвига из уравнения (5.45).
5.8.10. Нахождение сдвига Вычислите матрицу сдвига для сдвига, имеющего нормальный вектор m - 0,577(1, 1, 0) и угол ф = 45°. Нарисуйте все участвующие векторы и плоскость. Кроме того, нарисуйте, как этот сдвиг повлияет на куб с центром в начале координат и с ребрами, выровненными вдоль координатных осей.
5.8.11. Чем трехмерный сдвиг напоминает двумерное перемещение в однородных координатах?
Рассмотрим конкретный сдвиг:
