Используя разложение равенства (5.41)) запишите сдвиг в виде поворота, за которым следует масштабирование, а за ними - вновь поворот, чтобы убедиться в следующем: Произвольное двумерное аффинное преобразование - Перемещение х Поворот х

х Масштабирование х Поворот х Масштабирование х Поворот. (5.42)

Практические упражнения 5.8.1. «Золотое» разложение Рассмотрим частный случай «единичного сдвига», где элемент а - 1/а равенства (5.41) равен единице. Чему должно быть равно а? Определите два угла а и 3, связанные с этими поворотами.

petrocontrol.ru Расходомер Vzo оптом с доставкой в столице от дилера.

5.8. Тематические задания Решение.

Поскольку число а должно удовлетворять уравнению а - 1 + 1/а, оно является золотым соотношением ф\ Тогда

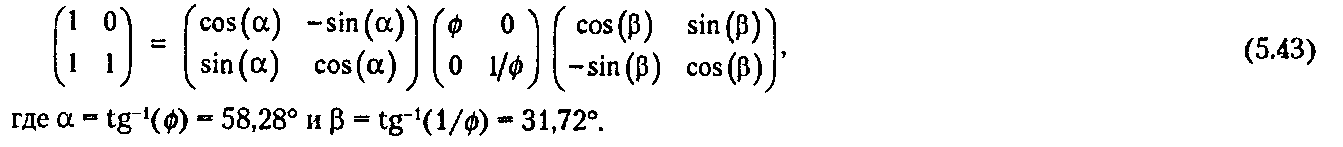
5.8.2. Единичные сдвиги Докажите, что любой сдвиг содержит в себе единичный сдвиг. Разложите сдвиг, заданный матрицей f 1 0^ h 1

на Произведение масштабирования, единичного сдвига и другого масштабирования.

5.8.3. Рисование вручную

испанская кухня алматы.

В соответствии с рассуждениями из упражнения 5.8.1 нарисуйте на миллиметровке прямоугольник, поверните его на -58,28°, масштабируйте его с множителями (ф, 1/ф) и, наконец, поверните его на 31,72°. Изобразите каждый промежуточный результат и покажите, что окончательный результат является тем же самым параллелограммом, что и исходный прямоугольник после единичного сдвига.

5.8.4. Разложение преобразования Разложите следующее преобразование:

Qx-3Px-2P,+ 5,
QrAPx+pr6

на произведение поворотов, масштабирований и перемещений.

5.8.5. Одно отражение может быть всегда от оси х

Докажите, что поворот на угол А вокруг начала координат всегда приводит к тому же эффекту, что и отражение от оси х с последующим отражением от прямой линии под углом А/2.

5.8.6. Изометрии Изометрии (isometries - «та же мера») являются отдельным важным семейством аффинных преобразований при исследовании симметрии, поскольку они не изменяют расстояние между двумя точками и их образами. Если преобразование Т( ) является изометрией, то для двух произвольных точек Р и Q расстояние \Т(Р) - T(Q)\ равно расстоянию \Р- Q\. Докажите, что если Г( ) - аффинное преобразование с матрицей М, то Гявляется изометрией тогда и только тогда, когда первые две строки матрицы М, рассматриваемые в качестве векторов, имеют единичную длину и ортогональны друг другу. Решение

⇐ Предыдущая| |Следующая ⇒