Преобразования объектов
Тематическое задание 5.2. Рисование звезды с рисунка 5.39 с помощью многократных поворотов Уровень сложности I.
Разработайте функцию, которая рисует полигон, изображенный на рис. 5.39, б, являющийся одной пятой частью звезды с рис. 5.39, а. Используйте этот полигон и преобразования поворота для того, чтобы нарисовать целую звезду.
Тематическое задание 5.3. Разложение двумерного аффинного преобразования Уровень сложности II.
Как мы уже видели, некоторые аффинные преобразования могут быть представлены в виде комбинации других аффинных преобразований. Здесь мы «разложим» произвольное аффинное преобразование на комбинацию из масштабирований, поворотов и перемещений. Мы также покажем, что поворот может быть выполнен посредством трех последовательных сдвигов, что приводит нас к очень быстрой подпрограмме рисования дуг. Кроме того, здесь рассматриваются некоторые скрытые особенности каждого трехмерного аффинного преобразования.
Поскольку аффинное преобразование является линейным преобразованием с последующим смещением, опустим ту часть аффинного преобразования, которая отвечает за перемещение, и сосредоточимся на его линейности. Таким образом, мы будем использовать упрощенные матрицы размерностью два на два.
Два двумерных линейных преобразования Рассмотрим матрицу M размерностью два на два, представляющую двумерное линейное преобразование. Матрицу M всегда можно разложить на множители поворота, масштабирования и сдвига. Обозначим для краткости четыре элемента матрицы M буквами а, Ъ, с, d. Убедитесь с помощью непосредственного умножения, что M является произведением следующих трех матриц [Martin, 137]:
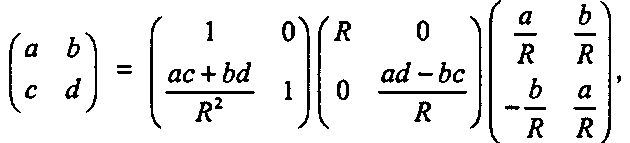
(5.39)где R = ^а2 + Ьг. Легко видеть, что крайняя матрица слева является сдвигом, средняя - масштабированием, а крайняя справа - поворотом. (Почему?) Следовательно, любое двумерное аффинное преобразование является поворотом, за которым следует масштабирование, а затем перемещение. Альтернативный вариант разложения рассматривается в тематическом задании 5.6.
