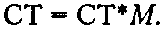
(5.37)
glMatrixMode(GL_MODELVIEW); glLoadldentityO:5.5. Использование аффинных преобразований в программах
// set СТ to the identity matrix
// устанавливаем СТ в матрицу тождественного преобразования }
//««««««« sca1e2D »»»»»»»»»» void Canvas:: seale2D(doublе sx. double sy) {
glMatrixMode(GL_MODELVIEW): glScaled(sx. sy. 1.0): // set CT to CT * (2D scaling)// устанавливаем CT - CT * (двумерное масштабирование) }
//«<«««««« translate2D »»»»»»»» void Canvas:: translate2D(double dx. double dy) {
g1 Matri xMode(GL_M0DELVIEW):glTranslated(dx, dy. 0): // set CT to CT * (2D translation) // устанавливаем CT - CT * (двумерное перемещение) }
//«««««««« rotate2D »»»»»»»»»»
void Canvas:: rotate2D(double angle)
{
g1 Ma t r|xMode(GL_M0DELVIEW):glRotated(angleT 0.0. 0.0. 1.0): // set CT to CT * (2D rotation) // устанавливаем CT - CT * (двумерный поворот) }
В листинге 5.1 приведены соответствующие определения четырех новых методов класса Canvas для управления текущим преобразованием, которые позволяют построить любые сложные двумерные преобразования. Столь приятная их простота связана с тем, что всю черновую работу выполняет OpenGL.
Теперь мы готовы к применению двумерных преобразований. Возвращаясь к рисованию домика № 2 с рис. 5.34, приведем код, который сначала поворачивает этот домик на -30° и затем перемещает его на вектор (32, 25). Отметим, что для получения прямого порядка следования этих операций они вызываются в порядке, обратном тому, в котором они применяются: сначала операция перемещения, а затем операция поворота.
cvs.setWindow(…):
cvs.setViewport(..):
// set the window to viewport mapping// настраиваем преобразование окно-порт просмотра
cvs.initCTO:// get started with the identity transformation // начинаем с тождественного преобразования houseO:
