Пример 5.3.3
Какая матрица соответствует лг-вращению на 45°, следующему за ним г/-вращению на 30° и последующему г-вращению на 60°? Непосредственное умножение трех составляющих матриц (обязательно в «обратном» порядке) дает следующий результат:
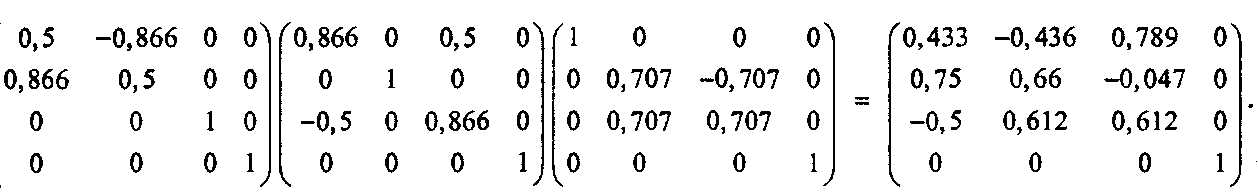
1 В честь Леонарда Эйлера (1707-1783), швейцарского математика необычайных способностей, внесшего неоценимый вклад во все разделы математики.
5.3. Трехмерные аффинные преобразования Иногда используют для создания сложного поворота другой порядок «вращений». Можно, например, выразить поворот в форме # (Р,) Я2(В2) КХФ3У- вначале дг-вращение, затем z-вращение и затем г/-вращение. В силу некоммутативности трехмерных поворотов для того, чтобы получить тот же самый поворот, для данного преобразования требуются другие углы Эйлера В,, В2 и В3. Всего существует 12 возможных порядков следования трех отдельных вращений, и в каждом из них используются различные величины В,, В2 и В3.
Повороты вокруг произвольной оси При использовании углов Эйлера мы выполняем последовательность х-, у- и г-вращений, то есть вращений вокруг координатных осей. Однако работать с поворотами было бы намного проще, если бы у нас была возможность осуществлять повороты вокруг произвольно направленной оси. Представьте себе Землю или игрушечный волчок, вращающиеся вокруг наклонной оси. В действительности в теореме Эйлера утверждается, что каждый поворот может быть представлен в такой форме.
Теорема Эйлера. Любой поворот (или последовательность поворотов) вокруг произвольной точки эквивалентен однократному повороту вокруг некоторой оси, проходящей через эту точку1.
Что же представляет собой матрица такого поворота и будет ли удобно с ней работать?
На рис. 5.28 показана ось, представленная вектором и, и произвольная точка Р, которая после поворота на угол В вокруг оси и должна перейти в точку Q. Поскольку вектор и может иметь любое направление, то на первый взгляд было бы затруднительно найти ту единственную матрицу, которая описывает такой поворот. Однако в действительности такая матрица может быть найдена двумя различными методами, так называемыми классическим (classic) и конструктивным (constructive).
