Рис. 4.53. Отсечение полигона по Сазерленду-Ходгману
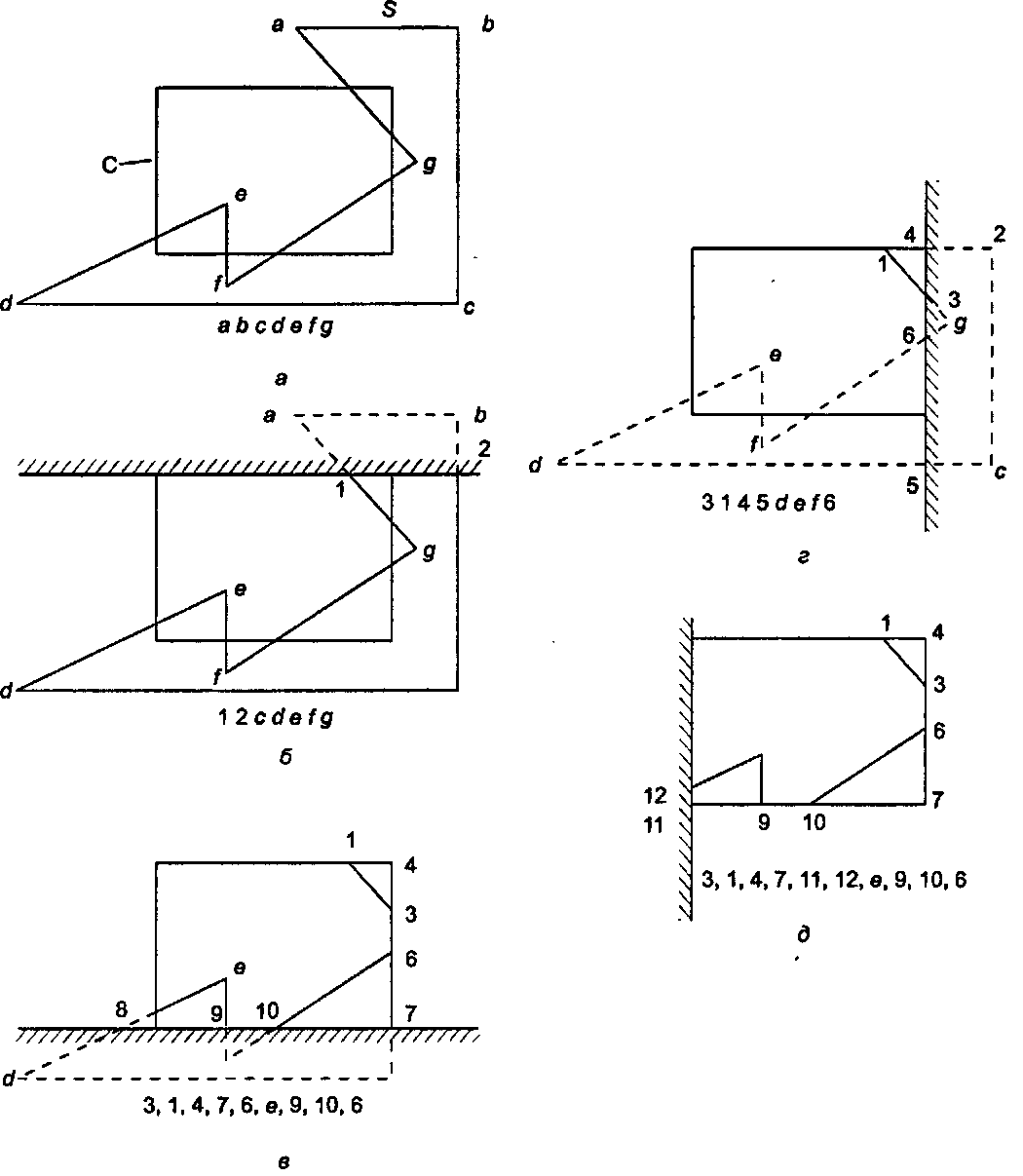
Теперь проследим за ходом работы алгоритма Сазерленда-Ходгмана по рис. 4.54. Рассмотрим отсечение полигона 5 верхним ребром прямоугольника С. Входной список вершин на этой стадии состоит из а, Ь, с, (1, е,/, g. Для удобства первым из списка берется то ребро, которое идет oтg к а, поскольку оно «соединяет» конец списка с его первым элементоМк Следовательно, здесь роль « играет точка £, а роль р - точка а. Ребро g, а (что означает ребро, идущее от точки g к точке а) пересекает отсекающее ребро в новой
4.10. Тематические задания точке «1», которая выводится в новый список. (Список вывода на каждой стадии алгоритма показан под соответствующим чертежом на рис. 4.54.) Следующим ребром во входном списке является а, Ъ. Поскольку обе конечные точки находятся выше отсекающего ребра, не выводится ничего. Третье ребро, Ь, с, дает на выходе сразу две точки, 2 и с, а четвертое ребро, с, й, выводит точку а*. Этот процесс продолжается до тех пор, пока не проверено последнее ребро, /, g, которое выводит точку g. Таким образом, новый список вершин для следующей стадии отсечения имеет вид"images/tmp8E4A-238.png" alt="Четыре случая для каждого ребра полигона S">
Рис. 4.54. Четыре случая для каждого ребра полигона S
Отметим, что образовались ненужные ребра (3,6 и 9,10), соединяющие три фрагмента полигона, созданные алгоритмом отсечения. Такие ребра могут вызвать проблемы в некоторых алгоритмах, осуществляющих заполнение полигонов. Удалить эти досаждающие ребра возможно, хотя и непросто [Sutherland, 193].
Реализуйте алгоритм отсечения Сазерленда-Ходгмана и протестируйте его на различных примерах полигонов. Пользователь с помощью мыши намечает выпуклый полигон С и затем таким же образом создает отсекаемый полигон 5. Каждый из них в момент создания рисуется красным цветом. Затем производится отсечение, и все отсеченные полигоны окрашиваются в синий цвет.