Вписанная окружность
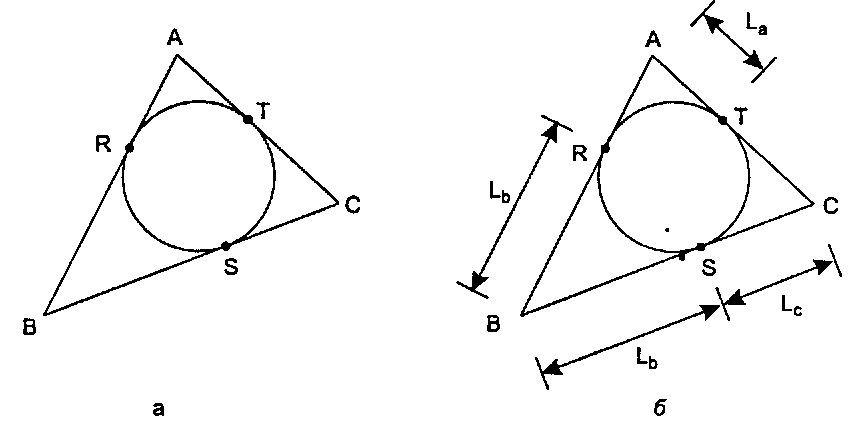
Это окружность, которая «устроилась» внутри заданного треугольника и касается всех трех его сторон1. На рис. 4.48, а показан треугольник ABC вместе с вписанной в него окружностью. Как было и в случае с описанной окружностью, труднее всего найти центр вписанной окружности. Прямой метод2 основывается на том, что окружность, вписанная в треугольник ABC, является описанной окружностью для другого треугольника, RST, вершины которого показаны на рисунке.
Рис. 4.48. Окружность, впитанная в треугольник ABC, является описанной окружностью для треугольника RST
Нам достаточно найти координаты точек R, S и Г и затем применить метод описанной окружности из «Приложение пересечения прямых: окружность, проходящая через три заданные точки». На рис. 4.48, б показаны расстояния от точек R, S и Гдо точек А, В и С. В силу симметрии окружности расстояния \В - R\ и \В - 5| должны быть равны друг другу, и существует еще две пары отрезков, имеющих одинаковую длину. Используя определения векторов а, Ь и с, согласно уравнению (4.56), имеем:
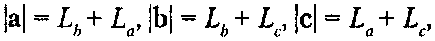
откуда с помощью перегруппировки можно выразить Ьа и Ьь:
21а-|а| + |с|-|Ь|; 2£4-|а| + |Ь|-|4 Зная Ьа и Ьь, находим:
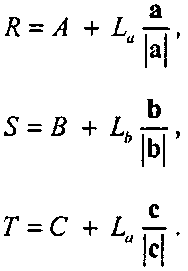
(4.66)(Проверьте эти выражения!)
1 Отмстим, что нахождение вписанной окружности попутно решает задачу нахождения единственной окружности, касательной к трем неколлипеарпым прямым на плоскости.
2 Предложен Расселом Сваном (Russell Swan).
Векторные инструменты для графики
Мы можем инкапсулировать вычисление точек Я, 5 и Г по точкам Л, Б и С в простой подпрограмме детЛапдег^РоШзСА. В. С, Р. Б. Т). Преимущество такого подхода состоит в том, что если у нас есть подпрограмма ехагс1е(), вычисляющая по трем точкам центр и радиус определяемой этими точками описанной окружности, то можно использовать ту же самую подпрограмму для вписанной окружности. Поэкспериментируйте с этими инструментами.
Девятиточечная окружность
В каждом треугольнике имеется девять замечательных точек: О середины трех сторон; О основания трех высот;
