Практическое упражнение 4.5.6. Рисование ломаной линии Нарисуйте на миллиметровке три точки: А, В и С. Для каждого значения t - 0,0,1,0,2,…, 0,9,1 вычислите положение P(t) из уравнения (4.38) и нарисуйте ломаную линию, проходящую через эти точки. Всегда ли это парабола?
4.5.6. Представление прямых и плоскостей Обратимся теперь к разработке главных математических форм, которые представляют прямые и плоскости. Вполне естественно найти внутри графической программы такие структуры данных, с помощью которых можно выразить прямую или плоскость.
Прямые в двумерном и трехмерном пространстве Прямая (line) определяется двумя точками, например Си В (рис. 4.25, а). Она не ограничена по длине, проходит через эти точки и бесконечно продолжается в обоих направлениях. Отрезок прямой (line segment) (для краткости - просто отрезок (segment)) также определяется двумя точками, а именно своими концевыми точками (endpoints), однако продолжается только от одной концевой точки до другой (рис. 4.25, б). Порождающая (parent) этот отрезок линия является бесконечной прямой, проходящей через его концевые точки. Луч (ray) является «полубесконечным» («semi-infinite»). Он определяется точкой и направлением, начинаясь в данной точке и простираясь бесконечно далеко в заданном направлении (рис. 4.25, в).
4,5, Отображение ключевых геометрических объектов
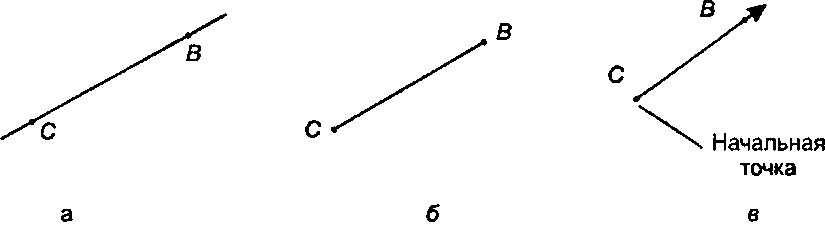
Рис. 4.25. Прямые, отрезки и лучи: а) прямая; б) отрезок прямой; в) луч
Эти объекты очень хорошо знакомы, тем не менее полезно собрать их важные представления и свойства в одном месте. Кроме того, мы опишем самое важное в компьютерной графике представление прямой: параметрическое представление (parametric representation).
Параметрическое представление прямой Структура, представленная в равенствах (4.36) и (4.37), очень полезна, поскольку по мере изменения параметра t точка Р проходит через все точки прямой линии, определяемой точками С и В. Следовательно, такая структура дает возможность указывать и вычислять любую точку прямой. Это делается с помощью параметра t, который отличает каждую точку прямой от другой точки. Пусть прямая обозначается L, тогда через L(t) обозначим положение точки на прямой, соответствующее t. Используя вектор Ь - В - С, получим:
