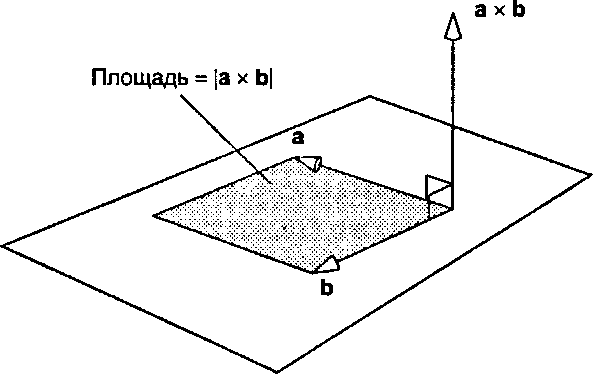
Рис. 4.15. Интерпретация векторного произведения Пример 4.4.2

Пусть а - (1,0,1), а Ь - (1,0,0). Эти векторы легко изобразить, так как оба они расположены в плоскости х - г. (Нарисуйте их.) Площадь параллелограмма, заданного векторами а и Ь, очевидно, равна единице. Поскольку вектор а х Ь ортогонален обоим векторам а и Ь, он должен быть параллельным оси у и, следовательно, пропорциональным ±]. Как в правосторонней, так и в левосторонней системе координат при повороте пальцев соответствующей руки от а к Ь большой палец указывает положительное направление оси у. Непосредственное вычисление согласно равенству (4.28) подтверждает правильность этих выводов, так как в данном случае а х Ь = ].

Практическое упражнение 4.4.7. Доказательство свойств Докажите три приведенные выше свойства векторного произведения.

4.4.2. Нахождение нормали к плоскости Как мы увидим в следующем разделе, иногда возникает необходимость вычислять компоненты вектора п, нормального к плоскости. Если известно, что эта плоскость проходит через три заданные точки, то эту задачу можно решить с помощью векторного произведения. Любые три точки Рх, Р2 и Р3 определяют единственную плоскость, если они не находятся на одной прямой. Это показано на рис. 4.16.

Для нахождения нормали к данной плоскости построим два вектора"images/tmp8E4A-192.png" alt="Нахождение плоскости по трем заданным точкам">

Рис. 4.16. Нахождение плоскости по трем заданным точкам Пример 4.4.3

Найдите вектор, нормальный к плоскости, проходящей через точки (1,0,2), (2,3,0) и (1,2,4). Решение Непосредственным вычислением получаем"opengl1_237.html">⇐ Предыдущая| |Следующая ⇒