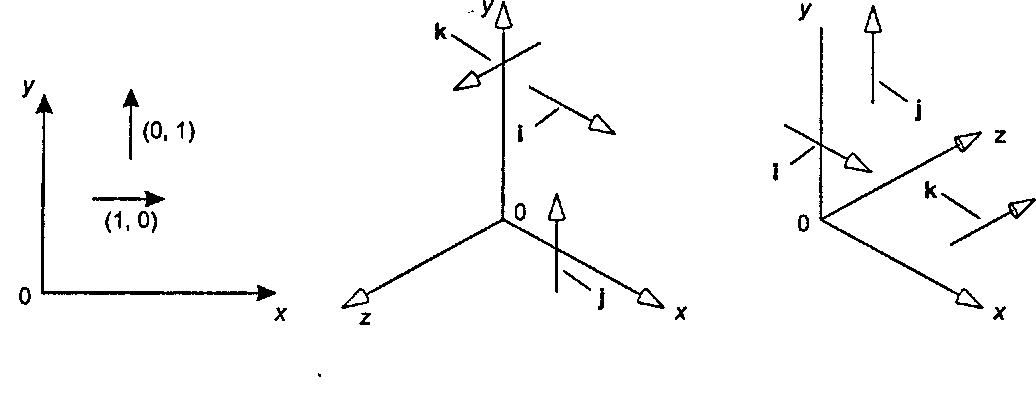
а б в Рис. 4.11. Координатные орты
Пример 4.3.4
Заметим, что v = (2,5, -1) - это то же самое, что 2(1,0,0) + 5(0,1,0) - 1(0,0,1), или 2i + 5j - к.
Форма записи, использованная в равенстве (4.19), представляет вектор в виде суммы отдельных элементарных составляющих векторов, что упрощает различные вычисления с помощью карандаша и бумаги. Эта форма записи особенно удобна при операциях с векторным произведением, к рассмотрению которого мы перейдем в разделе «Векторное произведение двух векторов».
Практические упражнения
4.3.1. Еще одно доказательство тождества b с = | b| | с | cos0
Отметим, что векторы b и с образуют две стороны треугольника, а его третья сторона равна b - с. Представьте, используя формулу косинусов, квадрат длины b - с через длины векторов b и с и косинус угла 6. Сравните свой ответ с равенством (4.12).
4.3.2. Нахождение угла Вычислите угол между векторами (2, 3) и (-3,1) и проверьте результат графически, с помощью миллиметровки. Затем вычислите угол между трехмерными векторами (1,3, -2) и (3,3,1).
4.3.3. Проверка на перпендикулярность
Какие пары из перечисленных ниже векторов перпендикулярны друг другу: (3,4,1), (2,1,1), (-3, -4,1), (0,0,0), (1, -2,0), (4,4,4), (0, -1,4) и (2,2,1)?
4.3.4. Теорема Пифагора Обратимся к равенствам (4.12) и (4.13). В случае перпендикулярности векторов а и b оба этих выражения - квадраты суммы и разности векторов - имеют одинаковую величину, что на первый взгляд не имеет геометрического смысла. Докажите, что все вычислено правильно, и примените полученный результат к теореме Пифагора.
4.3.4. Двумерный «перп» вектор
Пусть двумерный вектор а имеет компоненты (ах, ау). Какие векторы перпендикулярны к а? Один из способов получения такого вектора состоит в том, чтобы поменять местами х- и г/-компоненты и сменить у одного из них знак1. Пусть b = (-а , ах). В таком случае скалярное произведение а b = 0, поэтому а и b действительно перпендикулярны. Е*сли, к примеру, а = (4,7), то вектор b = (-7,4) является нор-
