Пример 4.3.2. Упрощение выражения | а - b 12

Упростить выражение для квадрата длины разности двух векторов а и b для получения равенства:

|а-Ь|2 - |а|2-2а-Ь+|Ь|2. (4.12)

Вывод этого соотношения делается так: обозначим буквой С выражение |а-Ь|2. Тогда, согласно четвертому свойству, С является скалярным произведением: С = |а-Ь|2 = (а-Ь)-(а-Ь).

купить ручки senator в Самаре.

Используя дистрибутивность, то есть раскрывая первые скобки, получим: С = а (а - b) - b (а - Ь). Исходя из свойств симметрии и линейности, упростим это выражение дальше: C = a- a-2a-b + b'b. Наконец, из четвертого свойства получаем С- |а|2- 2а b + |b|2, это и есть искомый результат.

Заменив в равенстве (4.12) знак минус на плюс, получим аналогичное полезное соотношение:

|а + Ь|2 - |а|2 + 2а b + |b|2. (4.13)

4.3.2. Угол между двумя векторами Наиболее важным применением скалярного произведения является нахождение угла между двумя векторами или между двумя пересекающимися прямыми. На рис. 4.9 приводится двумерный случай, когда векторы b и с расположены соответственно под углами фь и фс относительно оси х. Из элементарной тригонометрии известно, что

b = (flblcos^, |b|sin^); с - (|c|cos0c, |c|sin0c).

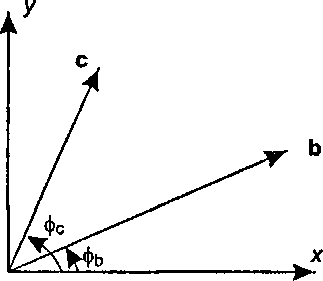
Рис. 4.9. Нахождение угла между двумя векторами Таким образом, скалярное произведение векторов Ь и с равно Ь с = \Ъ\\с\со5фсо5фь + |Ь||фіп06зіп0с = |Ь||с|соэ<0с - фь), следовательно, для любых двух векторов Ь и с получаем Ь с = |Ь||с|соб(Є), (4.14)

где 0 - угол между векторами Ь и с. Отсюда следует, что Ь с изменяется пропорционально косинусу угла между Ь и с. Этот же результат справедлив для трех, четырех и любого другого числа измерений.

Чтобы получить более компактную форму, разделим обе части равенства на |Ь||с|, а также используем запись единичного вектора в виде Ь = Ь/|Ь|. Тогда получим"opengl1_227.html">⇐ Предыдущая| |Следующая ⇒