Нашей работе в графике помогут две фундаментальные математические дисциплины: векторный анализ и преобразования. Изучая тонкости этих дисциплин, мы разработаем методы описания различных геометрических объектов, с которыми мы столкнемся, а также научимся переводить геометрические идеи в цифры. Результатом этого явится набор важных алгоритмов, к которым мы сможем обращаться в графических программах.

В данной главе мы изучим фундаментальные операции векторной алгебры и их применение в графике, а преобразования будут рассмотрены в главе 5. Мы начнем с самого начала и разработаем ряд важных инструментов и методов, которые будут встречаться нам снова и снова на протяжении всей книги. Если вы уже изучали векторы раньше, многое в этой главе будет вам знакомо, однако многочисленные приложения векторного анализа к геометрическим ситуациям все же следовало бы тщательно рассмотреть. Данная глава может показаться вам выпадающей из общей картины из-за обилия математического текста. Однако нам представляется весьма полезным иметь всю информацию, содержащуюся в ней, собранной в одном месте и отнесенной к реальным проблемам, встречающимся в графике.

7 Ф. Хилл

Векторные инструменты для графики

Почему векторы столь важны?

Обзор некоторых ситуаций, в которых на помощь приходит векторный анализ, может доказать необхо' димость изучения векторов. На рис. 4.1 приведены три геометрические задачи, возникающие в графи ке. Можно было бы привести много других примеров.

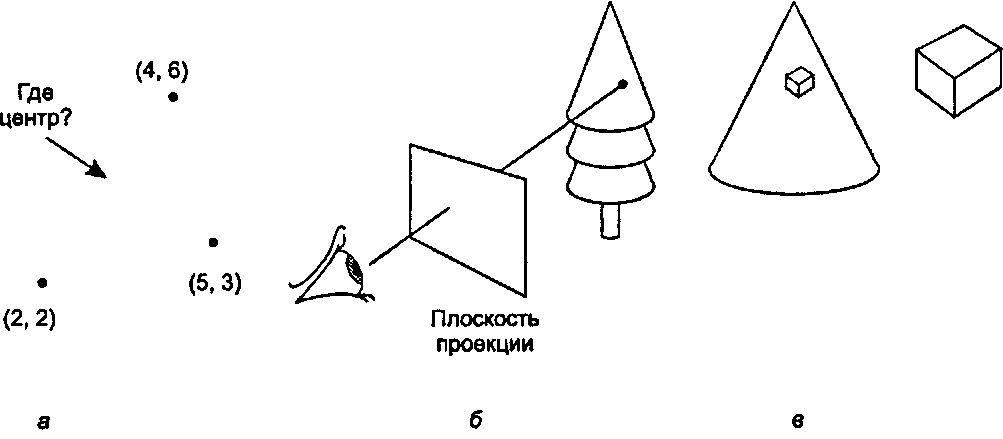
Рис. 4.1. Три примера геометрических задач, легко решаемых с помощью векторного анализа На рис. 4.1, а представлена задача компьютерного проектирования"opengl1_217.html">⇐ Предыдущая| |Следующая ⇒