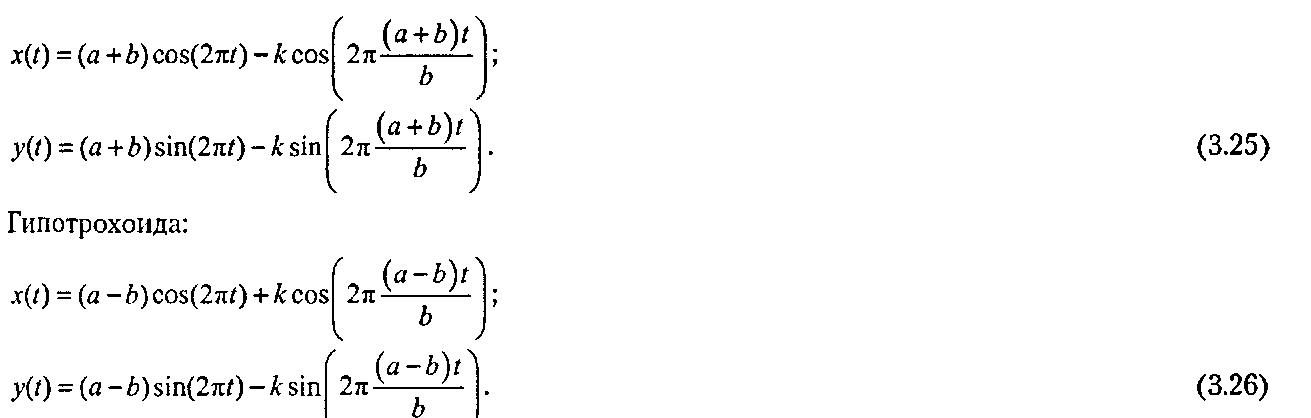
Гипоциклоида превращается в эллипс при а = 2ь для любого k.
1 Торговая марка фирмы Kenner Products.
Узнайте больше информации вот здесь онлайн.
Дополнительные инструменты для рисования
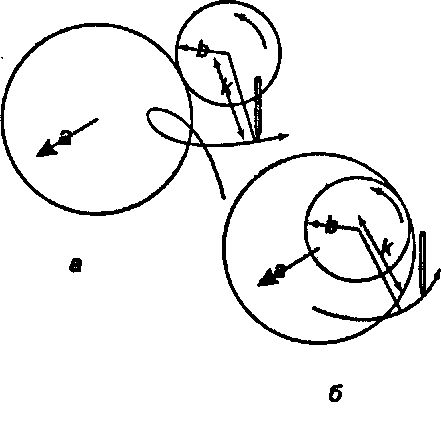
Рис 3.79. Окружности, вращающиеся вокруг окружностей Когда трассирующая точка лежит на вращающейся окружности (к - Ь), то описываемые ею кривые называются циклоидами (cycloids). Известны некоторые особые случаи циклоид, например эпициклоиды и гипоциклоиды.
Эпициклоиды"images/tmp8E4A-169.png" alt="Примеры циклоид">
Рис 3.80. Примеры циклоид: а) нефроида; б) а/b = 10; в) дельтоида; г) астроида Тематическое задание 3.9. Суперэллипсы
Уровень сложности I.
Напишите и выполните программу для рисования суперэллипсов. Чтобы нарисовать каждый суперэллипс, пользователь назначает противоположные углы ограничивающего прямоугольника и набирает значение выпуклости (bulge), после чего рисуется заданный суперэллипс.
1 Отметим, что астроида является в то же время и суперэллипсом! Ее кривизна равна 2/3.
3.11. Дополнительная литература
(Факультативно.) Усовершенствуйте свою программу таким образом, чтобы она могла рисовать повернутые суперэллипсы. Пользователь набирает значение угла после ввода выпуклости.
3.11. Дополнительная литература В начале работы с графикой большое удовольствие доставляет писать приложения, дающие на выходе замечательные кривые и орнаменты. Это приводит вас к пониманию глубокой взаимосвязи между математикой и изобразительным искусством. Имеется множество книг, готовых предложить вам руководство и мириады примеров. Книга Мак-Грегора и Уоттса «Искусство графики для IBM PC* (McGregor and Watt's. The Art of Graphics for the IBM PC [Mcgregor, 138]) предлагает множество алгоритмов для создания интересных орнаментов. Вот еще несколько заслуживающих особого внимания книг о кривых и геометрии: Джей Каппраффс «Соединения» (Jay Kappraff Connections [Kappraff, 121]), А. К. Дьюдни «Мир кресел» (А. К. Dewdney. The Armchair Universe [Dewdney, 58]), Стен Огилви «Экскурсии в геометрию» (Stan Ogilvy Excursions in Geometry [Ogilvy, 148]), Д. Педо «Геометрия и изобразительное искусство» (D. Pedoe Geometry and the Visual Arts [Pedoe, 155]), Роджер Шеперд «Взгляды разума» (Roger Sheperd Mind Sights [Sheperd, 184]), а также целый ряд книг о математических путешествиях Мартина Гарднера (Martin Gardner), такие как «Путешествие во времени» (Time Travel [Gardner, 77]) и «Мозаики Пенроуза для шифровых замков» Penrose Tiles to Trapdoor Ciphers [Gardner, 78]). Коксетером (Coxeter) написаны элегантные книги по геометрии, в том числе «Введение в геометрию» (Introduction to Geometry [Coxeter, 51]). В книгах «Математические развлечения и эссе» (Mathematical Recreations and Essays [Ball, 8]) и «Математика для компьютерной графики» Хоггара (Hoggar. Mathematics for Computer Graphics [Hoggar, 112]) рассматриваются многие свойства IFS.
