moveToCfirst.x. first.у): // to world CP // для внешних CP
int sx = (intHmapA * second.x + mapC):int sy = (intXmapB * second.у + mapD):
lineto(sx.sy): //a Turbo С++ routine // подпрограмма Turbo С++ }
moveTo(x. y): // update CP // обновляем CP }
Напишите полную реализацию класса Canvas на Turbo С++ (или в подобной программной среде, которая требует от вас реализовывать отсечение и преобразование). Разберитесь должным образом с установкой цветов рисования и фона (данная операция обычно сильно зависит от системы). Протестируйте свой класс, использовав его в приложении, которое рисует полиспирали, задаваемые пользователем.
Тематическое задание 3.4. Рисование арок Уровень сложности И.
Арки использовались в архитектурных композициях на протяжении всей истории строительства. Их структурная прочность и декоративная простота делают их чрезвычайно важными элементами структурного проектирования, поэтому большое разнообразие подобных форм входят в состав церквей, мостов, порталов и т. д.
На рис. 3.69 показаны две основные формы арок. Арка на рис. 3.69, а с центром в начале координат имеет ширину 2 W. Эта арка начинается на высоте Я над основанием. Ее основным элементом является полукруг с радиусом R = W. Отношение H/W может быть задано по желанию. Например, H/W может быть связано с золотым отношением.
3.10. Тематические задания
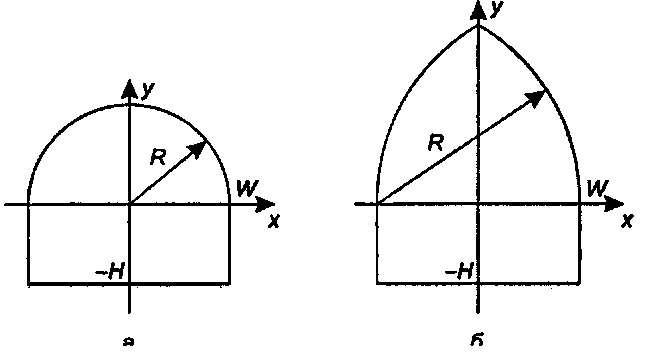
Рис. 3.69. Две основные арочные формы: а) закругленная арка; б) стрельчатая арка На рис. 3.69, б показан идеализированный вариант второй из широко известных арочных форм, называемой «стрельчатой» («pointed»), или «равнобочной» («equilateral»), аркой, которую часто можно видеть в соборах1. Здесь два арки радиуса R - 2"/сходятся точно над центром. (Чему равен угол развертки каждой арки?)
Арка под названием «гусек»2 (или «килевидная» - «keel») показана на рис. 3.70. Такая арка впервые появилась около 1300 года н. э. и была популярным архитектурным элементом на протяжении всего позднего средневековья. В верхней части полукруглой арки радиуса R располагаются два круга радиуса fR, где / - некоторая дробь. Такая структура определяет положение этих двух кругов. (Какие координаты имеет точка С?) На каждой стороне обе дуги сопрягаются вместе, образуя плавную остроконечную вершину. Интересно определить параметры различных арок в терминах Wnf.
