f(x)-4Xx(l-x), (3.24)где X - некоторая константа, выбранная из промежутка от 0 до 1. При итеративном применении функции /(.), начиная с заданной точки х0 (также из промежутка от 0 до 1), генерируется орбита (orbit) (вспомните определение этого термина в главе 2): Как ведет себя эта последовательность? Здесь таится много сложностей. Поведение данной последовательности можно сделать более наглядным, если определенным образом отобразить его графически. На рис. 3.67 показана парабола у - 4Хх(1 - х) для X - 0,7 при изменении х от 0 до 1.
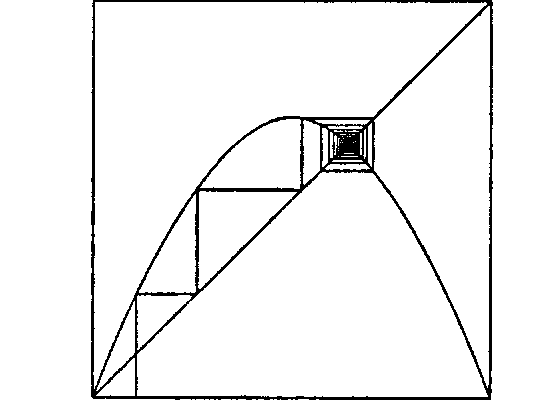
Рис 3.67. Логистическое преобразование для А = 0,7
Дополнительные инструменты для рисования
Здесь выбрана начальная точка х0 - 0,1, и в этой точке проведена вертикальная линия до параболы, что дало величину /(х0) - 0,252. Далее нам следует применить рассматриваемую функцию к новой величине х1 - 0,252. Это наглядно демонстрируется с помощью горизонтального движения до прямой у - х, как показано на рисунке. Затем, чтобы выяснить значение функции/( ) в этой новой точке, снова проводим вертикальную линию до параболы. Данный процесс повторяется бесконечно, как у всякой системы итерируемых функций. Из предыдущей точки с координатами (хк_,, хк) проводится горизонтальная линия к точке (хк, хк), откуда проводится вертикальная линия к точке (хк,хк+1). Из рисунка видно, что при Я. - 0,7 эти величины быстро сходятся к постоянному «аттрактору» - фиксированной точке, в которой /(#) - х. (Каково значение этой точки при X - 0,7?) Заметим, что этот аттрактор не зависит от начальной точки: последовательность всегда быстро сходится к конечной величине.
Исследуем, как можно управлять этим процессом, задавая различные значения параметра X, то есть покрутим «А,-рукоятку». Если А, мало, то процедура будет даже проще: единственный аттрактор обнаружится при х = 0. Однако когда значение «Х-рукоятки» увеличивается, начинает твориться что-то странное. На рис. 3.68, а показано, что происходит при X = 0,85. «Орбита», представляющая нашу последовательность, превращается в бесконечно повторяющийся цикл, никогда не сходящийся к конечной величине. Здесь имеется несколько аттракторов, по одному на каждой вертикальной линии в предельном цикле, показанном на рисунке. А когда X становится больше критического значения Я. = 0,892486418…, процесс становится воистину хаотическим.
