На рис. 3.59, а показано семейство суперокружностей (supercircles), частного случая суперэллипсов при W = Н. На рис. 3.59, б приведена сцена, полностью составленная из суперэллипсов и демонстрирующая диапазон их возможных форм.
При п > 1 выпуклость направлена наружу, а при п < 1 - вовнутрь. Когда п = 1, суперокружность превращается в квадрат. (В главе 6 мы рассмотрим трехмерные «суперквадрикн» (superquadrics) - поверхности, которые иногда используют в системах автоматического проектирования для моделирования объемных тел.)
Суперэллипсы были впервые исследованы в 1818 году французским физиком Габриэлем Ламэ (Gabriel Lame). Позже, 1959 году, выдающийся изобретатель Пит Хайн (Piet Hein) (больше всего известный как создатель куба Soma и игры Hex) решал задачу проектирования кольцевой транспортной развязки (traffic circle) в Стокгольме. Окружность кольцевой трассы должна была вписаться в прямоугольник (с отношением сторон W/H = 6/5), который определялся другими дорогами, и должна была обеспечить плавный транспортный поток, а также быть приятной для глаз. Эллипс получался слишком
Рис. 3.58. Знакомый «глаз», построенный из кругов и эллипсов
3.8.3. Суперэллипсы
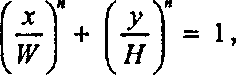
(3.17)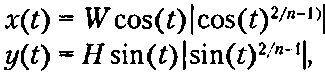
(3.18)Дополнительные инструменты для рисования
заостренным на концах для транспортной магистрали, поэтому Хейн искал более плоскую кривую с более прямыми сторонами и подумал о суперэллипсе. Он выбрал п = 2,5, при котором выпуклость была наиболее подходящей. Стокгольм мгновенно принял идею суперэллипса для своего нового центра. Эти кривые были «удивительно подходящими, ни слишком круглыми, ни слишком угловатыми, удачное сочетание красоты эллипсов и прямоугольников» [Gardner, 78, с. 243]. С тех пор формы суперэллипсов появились в мебели, текстильных орнаментах и даже в столовом серебре. Более подробно о них написано в книгах [Gardner, 78] и [Hill, 109].
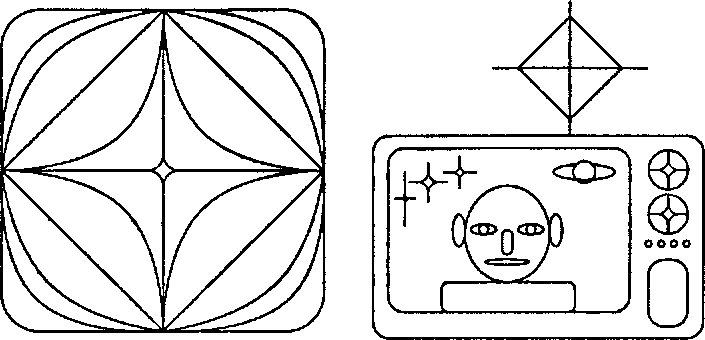
а б Рис. 3.59. Семейство суперокружносгей (а); сцена, созданная из суперэллипсов (5)
Аналогичным образом может быть определена супергипербола (superhyperbola) [Barr, 13]. Достаточно заменить в равенстве (3.18) cos(f) на sec(c) и sin (с) на tg(t). При п = 2 получается обычная гипербола. На рис. 3.60 показано несколько примеров супергипербол. Когда выпуклость п становится больше 2, кривая выпячивается наружу все больше и больше, а когда выпуклость уменьшается, кривая выпячивается все меньше и меньше, становясь прямой при п = 1 и прогибаясь внутрь при п < 1.